3  Potential outcomes and counterfactuals

Work-in-progress 🚧

You are reading the work-in-progress first edition of Causal Inference in R. This chapter is mostly complete, but we might make small tweaks or copyedits.

Two roads diverged in a yellow wood,
And sorry I could not travel both
And be one traveler, long I stood
And looked down one as far as I could
To where it bent in the undergrowth
— Robert Frost

In 2022, Ice-T, best known as an American rapper and Fin on Law and Order: SVU, co-authored a book titled Split Decision: Life Stories (Century 2022). In Split Decision, Ice-T recounts his dramatic journey from a life of crime to fame and success, contrasting it with the fate of his former crime partner and co-author, Spike. Both men grew up in gang-dominated neighborhoods in Los Angeles and committed jewelry heists together. Their lives diverged when Ice-T was discovered rapping in a club. This led him to leave behind his criminal past and launch a successful career in music, film, and television. Meanwhile, Spike was caught in a jewelry robbery and imprisoned for three years. He continued his life of crime, culminating in a botched robbery that led to a 35-year to life prison sentence. The book’s copy describes how “two men with two very different lives reveal how their paths might have very well been reversed if they had made different choices.”

This compelling premise implies that we are observing counterfactuals: two lives that follow the same trajectory until one decision (one more heist vs. pursuing a music career) diverges them: in one life, jail, and in another, success and fame. The book begins by setting up all the ways Ice-T and his friend Spike were similar before this divergence (e.g., they both grew up in Los Angeles neighborhoods, were involved with gangs, and worked together to orchestrate a series of jewelry heists). Then something happens: Ice-T abandons criminal life, and Spike makes the opposite decision. What happens next for Ice-T includes fame and fortune, while Spike ends up with 35 years to life in prison. This book attempts a small study of two people who were the same before an event and different after it. Spike’s outcomes serve as the counterfactual to Ice-T’s.

flowchart LR
A{Ice-T} --> |observed| B(Abandons criminal life)
A -.-> |missing counterfactual| C(Does one more heist)
C -.-> D[35 years in prison]
B --> E[Fame & Fortune]

classDef grey fill:#ddd
class D,C grey

flowchart LR
A{Spike} -.-> |missing counterfactual| B(Abandons criminal life)
A --> |observed| C(Does one more heist)
C --> D[35 years in prison]
B -.-> E[Fame & Fortune]
classDef grey fill:#ddd
class E,B grey

Table 3.1: Ice-T and Spike Causal Map. For the two men, we have only one observed outcome. Their memoir implies that each is a good counterfactual for the other. Had Ice-T continued with heists, would he have ended up in jail? If Spike had quit heists, would he have had fame and fortune?

We don’t know what would have happened to Ice-T had he continued partnering with Spike on heists. We also don’t know what would have happened to Spike if he had avoided crime like Ice-T. We live in a single factual world where Ice-T left crime, and Spike didn’t. Yet, we can see how the two men can be each other’s proxies for those counterfactual outcomes. In causal inference techniques, we attempt to use observed data to simulate counterfactuals in much the same way. Even randomized trials are limited to a single factual world, so we compare the average effects of groups with different exposures.

Nevertheless, there are several issues that we can immediately see, highlighting the difficulty in drawing such inferences. First, while the book implies that the two individuals were similar before the decisions that diverged their fates, we can guess how they might have differed. Would one more heist have led Ice-T to prison? It’s easier to see Spike as a good counterfactual here. What about the other way around: if Spike had quit crime, would he have become a famous musician and actor? Ice-T decided to leave his life of crime, but that wasn’t the only factor in his success: he had enough musical talent to make a career of it. Did Spike have Ice-T’s musical talent? Can we conclude that his life would have turned out exactly like Ice-T’s if he had made the same choices? If we want to truly estimate the causal effect of Ice-T’s decision to leave criminal life on his future outcomes, we would need to observe his ultimate course both before and after making the decision. Similarly, Spike might be different from Ice-T in hard-to-measure ways, which makes him a poorer poxy for Ice-T’s counterfactuals than he first seems. Instead of relying on a single individual, we often rely on many. We could conduct an experiment in which we randomize many individuals to leave criminal life (or not) and see how this impacts their outcomes on average (of course, this randomized trial presents some ethical issues, which is why observational data like Ice-T and Spike’s are interesting). In any case, we must rely on statistical techniques to help construct these unobservable counterfactuals from observed data.

3.1 Potential outcomes

Factual outcomes and counterfactual outcomes are two realizations of potential outcomes. Before some cause occurs, the potential outcomes are all the things that could happen depending on what you are exposed to. Let’s say that the cause we are interested in is a particular moment in the 1980s when one decides to either quit doing jewel heists or continue. The outcome we’re interested in is whether or not the individual goes to jail.

Let’s assume an exposure has two levels:

• \(X=continue\) if you continue doing jewel heists

• \(X=quit\) if you quit doing jewel heists

Under this scenario, there are two potential outcomes:

• \(Y(continue)\), the potential outcome if \(X=continue\)

• \(Y(quit)\), the potential outcome if \(X=quit\)

Only one of these potential outcomes will be realized, the factual one corresponding to the exposure that actually occurred. Therefore, only one potential outcome is observable for each individual. These exposures are defined at a particular time (in this case, a specific moment in the 1980s, right around the time Ice-T was discovered), so only one can happen to any individual. In the case of a binary exposure, this leaves one potential outcome as observable and one missing. In fact, early causal inference methods were often framed as missing data problems; we need to make certain assumptions about the missing counterfactuals, the value of the potential outcome corresponding to the exposure(s) that did not occur.

Our causal effect of interest is often some difference in potential outcomes, such as \(Y(continue) - Y(quit)\) (say, the difference in the probabilities of going to jail the following year if you continue heists vs. quitting heists). In the case of Ice-T and Spike, we’re interested in their individual causal effects:

• \(Y_{Ice-T}(continue) - Y_{Ice-T}(quit)\)
• \(Y_{Spike}(continue) - Y_{Spike}(quit)\)

Here, we’re missing \(Y_{Ice-T}(continue)\) and \(Y_{Spike}(quit)\), so we can’t calculate these values. In practice, we need to use observed data as proxies for the missing potential outcomes, and we usually average them over a particular population. To do this, though, we can’t just throw some statistics at a pile of observed data; we need to meet certain causal assumptions that allow us to imbue observed data with the meaning of potential outcomes and their analysis with causal effects.

Counterfactuals as potential outcomes

In this book, we use the terms potential outcomes and counterfactuals more or less interchangeably, but they are not technically identical in their meaning. A counterfactual is a type of potential outcome, referring to a potential outcome that was not realized and is thus unobservable. The definition of a counterfactual depends on the exposure that actually happened. Potential outcomes, though, are agnostic to the observed exposure and are often well-defined before it even happens. Nevertheless, we usually work with data after an exposure happens, so we have one realized potential outcome and at least one potential outcome that is counter to the fact. Some die-hards insist on one term or the other, but we find both useful.

Let’s consider a different example: the effect of ice cream on happiness.

3.1.1 Does chocolate ice cream make you happier than vanilla?

Let’s suppose some happiness index exists that ranges from 1-10. We want to assess whether eating chocolate ice cream versus vanilla will increase happiness. We have 10 individuals with two potential outcomes for each. One is their happiness if they ate chocolate ice cream (defined as y_chocolate in the code below), and one is their happiness if they ate vanilla ice cream (y_vanilla). We can define the true individual causal effect of eating chocolate ice cream (versus vanilla) on happiness for each individual as the difference between the two (Table 3.2).

data <- tibble(
  id = 1:10,
  y_chocolate = c(4, 4, 6, 5, 6, 5, 6, 7, 5, 6),
  y_vanilla = c(1, 3, 4, 5, 5, 6, 8, 6, 3, 5)
)

data <- data |>
  mutate(causal_effect = y_chocolate - y_vanilla)

library(gt)
data |>
  gt() |>
  cols_label(
    id = "ID",
    y_chocolate = md("$$Y_{\\text{id}}(\\text{chocolate})$$"),
    y_vanilla = md("$$Y_{\\text{id}}(\\text{vanilla})$$"),
    causal_effect = md("$$Y_{\\text{id}}(\\text{chocolate}) - Y_{\\text{id}}(\\text{vanilla})$$")
  ) |>
  fmt_markdown(
    columns = c(y_chocolate, y_vanilla, causal_effect)
  ) |>
  tab_header(
    title = md("**Potential Outcomes and Causal Effect**")
  ) |>
  tab_spanner(
    label = "Potential Outcomes",
    columns = c(y_chocolate, y_vanilla)
  ) |>
  tab_spanner(
    label = "Causal Effect",
    columns = causal_effect
  )

Potential Outcomes and Causal Effect
ID	Potential Outcomes		Causal Effect
	\[Y_{\text{id}}(\text{chocolate})\]	\[Y_{\text{id}}(\text{vanilla})\]	\[Y_{\text{id}}(\text{chocolate}) - Y_{\text{id}}(\text{vanilla})\]
1	4	1	3
2	4	3	1
3	6	4	2
4	5	5	0
5	6	5	1
6	5	6	-1
7	6	8	-2
8	7	6	1
9	5	3	2
10	6	5	1

Table 3.2: Potential Outcomes Simulation: The causal effect of eating chocolate (versus vanilla) ice cream on happiness. In this simulation, each individual has a known outcome for each exposure. Since we know each potential outcome, we can calculate the individual causal effects on happiness of eating chocolate versus vanilla ice cream.

For example, examining Table 3.2, the causal effect of eating chocolate ice cream (versus vanilla) for individual 4 is 0, whereas the causal effect for individual 9 is 2.

The average potential happiness after eating chocolate is 5.4, and the average potential happiness after eating vanilla is 4.6. The average treatment effect of eating chocolate (versus vanilla) ice cream among the ten individuals in this study is 5.4 - 4.6 = 0.8.

data |>
  summarize(
    avg_chocolate = mean(y_chocolate),
    avg_vanilla = mean(y_vanilla),
    avg_causal_effect = mean(causal_effect)
  )

# A tibble: 1 × 3
  avg_chocolate avg_vanilla avg_causal_effect
          <dbl>       <dbl>             <dbl>
1           5.4         4.6               0.8

In reality, we cannot observe both potential outcomes at any given moment; each individual in our study can only eat one flavor of ice cream at the moment of study¹. Suppose we randomly gave one flavor or the other to each participant. Now, what we observe is shown in Table 3.3. We only know one potential outcome (the one related to the exposure the participant received). We don’t know the other one, and consequently, we don’t know the individual causal effect.

## we are doing something *random* so let's
## set a seed so we always observe the
## same result each time we run the code
set.seed(11)
data_observed <- data |>
  mutate(
    # change the exposure to randomized, generated from
    # a binomial distribution with a probability of 0.5 for
    # being in either group
    exposure = case_when(
      rbinom(n(), 1, 0.5) == 1 ~ "chocolate",
      TRUE ~ "vanilla"
    ),
    observed_outcome = case_when(
      exposure == "chocolate" ~ y_chocolate,
      exposure == "vanilla" ~ y_vanilla
    )
  )

avg_chocolate <- data_observed |>
  filter(exposure == "chocolate") |>
  pull(observed_outcome) |>
  mean()

avg_vanilla <- data_observed |>
  filter(exposure == "vanilla") |>
  pull(observed_outcome) |>
  mean()

data_observed |>
  mutate(
    y_chocolate = ifelse(exposure == "chocolate", y_chocolate, NA),
    y_vanilla = ifelse(exposure == "vanilla", y_vanilla, NA),
    causal_effect = NA_real_
  ) |>
  select(-observed_outcome, -exposure) |>
  gt() |>
  cols_label(
    id = "ID",
    y_chocolate = md("$$Y_{\\text{id}}(\\text{chocolate})$$"),
    y_vanilla = md("$$Y_{\\text{id}}(\\text{vanilla})$$"),
    causal_effect = md("$$Y_{\\text{id}}(\\text{chocolate}) - Y_{\\text{id}}(\\text{vanilla})$$")
  ) |>
  fmt_markdown(columns = c(y_chocolate, y_vanilla, causal_effect)) |>
  sub_missing(
    columns = c(y_chocolate, y_vanilla, causal_effect),
    missing_text = md("---") # Format missing values as blank
  ) |>
  tab_header(
    title = md("**Potential Outcomes and Hidden Causal Effect**")
  ) |>
  tab_spanner(
    label = "Potential Outcomes",
    columns = c(y_chocolate, y_vanilla)
  ) |>
  tab_spanner(
    label = "Causal Effect",
    columns = causal_effect
  )

Potential Outcomes and Hidden Causal Effect
ID	Potential Outcomes		Causal Effect
	\[Y_{\text{id}}(\text{chocolate})\]	\[Y_{\text{id}}(\text{vanilla})\]	\[Y_{\text{id}}(\text{chocolate}) - Y_{\text{id}}(\text{vanilla})\]
1	—	1	—
2	—	3	—
3	6	—	—
4	—	5	—
5	—	5	—
6	5	—	—
7	—	8	—
8	—	6	—
9	5	—	—
10	—	5	—

Table 3.3: Potential Outcomes Simulation: The observed exposure is the only potential outcome we know. We don’t know the missing potential outcome, and thus, we cannot calculate the individual causal effect. We need to use the observed exposure and outcome to estimate the effect of eating chocolate (versus vanilla) ice cream on happiness. Unfortunately, we can’t do it at the individual level.

Now, the observed average outcome among those who ate chocolate ice cream is 5.3, while the observed average outcome among those who ate vanilla is 4.7. These are close to the actual averages, even though we are now missing the counterfactual outcomes. The estimated average causal effect is 5.3 - 4.7 = 0.6. We’re a little off because of the low sample size, but we would get a more exact answer as the sample size increased.

data_observed |>
  group_by(exposure) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 2 × 2
  exposure  avg_outcome
  <chr>           <dbl>
1 chocolate        5.33
2 vanilla          4.71

Why does this work even though we can no longer calculate the true causal effect? Randomization, it turns out, has the properties we need to meet causal assumptions about observed data. Because these assumptions are met, we can use the observed averages as proxies for the averages of the two potential outcomes.

Let’s see why this is and what happens when those assumptions are violated.

3.2 Causal assumptions

We’ll discuss many methods throughout this book. Each method comes with unverifiable assumptions that we need to interpret the results as causal. These assumptions have one goal: to allow us to use observed data to represent unobservable counterfactuals. What does it require for us to be able to do this?

Apples-to-apples

Most of the assumptions we need to make for causal inference are to make an apples-to-apples comparison: We want to compare similar individuals who would serve as reasonable proxies for each other’s counterfactuals.

The phrase “apples-to-apples” comes from the saying “comparing apples to oranges,” which means comparing two incomparable things.

That’s only one way to say it. There are a lot of variations worldwide. Here are some other things people incorrectly compare:

• Cheese and chalk (UK English)
• Apples and pears (German)
• Potatoes and sweet potatoes (Latin American Spanish)
• Grandmothers and toads (Serbian)
• Horses and donkeys (Hindi)

For the first three-fourths or so of the book, we’ll deal with so-called unconfoundedness methods. These methods all assume² three things: exchangeability, positivity, and consistency. We’ll focus on these three assumptions for now, but other methods, such as instrumental variable analysis (Chapter 22) and difference-in-differences (Chapter 23), make other causal assumptions. Knowing a method’s assumptions is essential for using it correctly, but it’s also worth considering if another method’s assumptions are more feasible for the problem you are trying to solve.

These assumptions are sometimes called identifiability conditions since we need them to hold to identify causal estimates. Likewise, you’ll sometimes see people discussing whether or not a given causal effect is “identifiable.”

3.2.1 Exchangeability

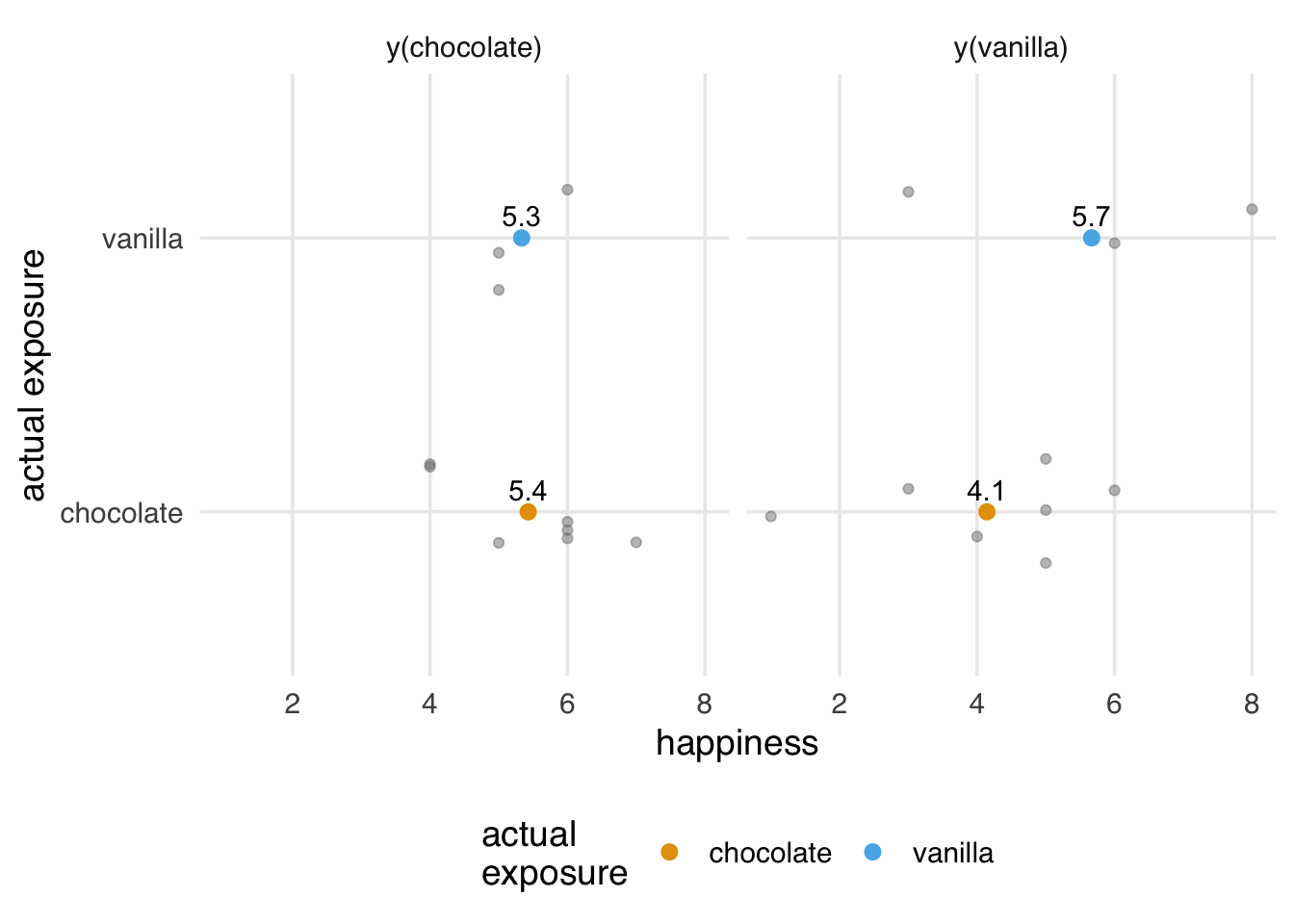
The exchangeability assumption is the hallmark of unconfoundedness methods like inverse probability weighting and regression adjustment. Here, we assume that each exposure group has the same potential outcomes on average. So, the group that was assigned “chocolate” ice cream has the same potential outcomes for happiness for chocolate as the vanilla group (had they been assigned to chocolate). Mathematically, exchangeability is written as \(Y(x) \perp\!\!\!\perp X\). Exposure status is independent of the potential outcomes; being in the chocolate group, for instance, doesn’t change your potential outcome y(chocolate) compared to being in the vanilla group. When this assumption holds, we can treat the vanilla group as the proxy for the chocolate group’s y(vanilla) and vice versa, as in Figure 3.1.

data_observed |>
  select(starts_with("y"), exposure) |>
  pivot_longer(
    starts_with("y"),
    names_prefix = "y_",
    names_to = "potential_outcome",
    values_to = "happiness"
  ) |>
  mutate(potential_outcome = paste0("y(", potential_outcome, ")")) |>
  ggplot(aes(happiness, exposure, color = exposure)) +
  geom_jitter(width = 0, height = .2, alpha = .5, color = "grey50") +
  stat_summary(fun = "mean", size = 2.5, geom = "point") +
  stat_summary(
    fun = "mean",
    geom = "text",
    aes(label = round(after_stat(x), 1)),
    vjust = -0.6,
    color = "black"
  ) +
  facet_wrap(~potential_outcome) +
  labs(y = "actual exposure", color = "actual\nexposure")

Figure 3.1: The average potential outcomes by observed exposure group. Under exchangeability, the exposure groups have nothing to do with the potential outcomes. Had the vanilla group received chocolate, their potential outcomes would have been about the same on average as the chocolate group, and vice versa. Exchangeability allows us to use each group as a counterfactual for the other.

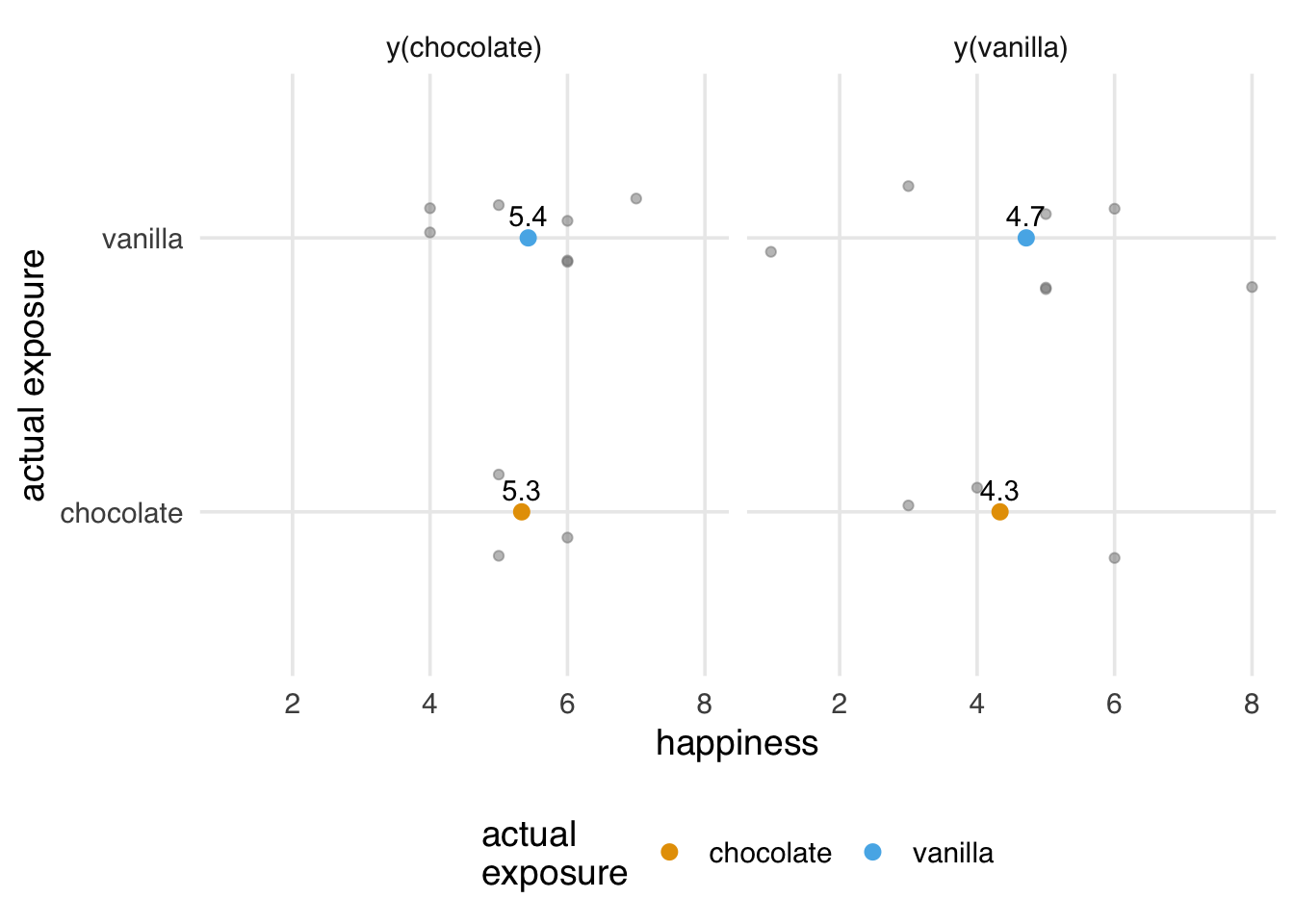
Exchangeability is sometimes called the “no confounding” or “unconfoundedness” assumption. It’s also sometimes called “ignorability.”

Exchangeability is guaranteed in the limit when you randomize the exposure, as we did earlier with ice cream flavors. You can see where the name comes from by considering exchangeability from a randomization process. Let’s say we mixed up the labels for who got which flavor, and we accidentally gave chocolate to the “vanilla” group and vanilla to the “chocolate” group. Because flavor assignment is independent of the potential outcomes, this mix-up doesn’t matter. We’ve exchanged the groups by flipping their assignments, but we can still detect the right causal effect ³.

set.seed(11)

mix_up <- function(flavor) {
  ifelse(flavor == "chocolate", "vanilla", "chocolate")
}

data_observed <- data |>
  mutate(
    exposure = case_when(
      rbinom(n(), 1, 0.5) == 1 ~ "chocolate",
      TRUE ~ "vanilla"
    ),
    exposure = mix_up(exposure),
    observed_outcome = case_when(
      exposure == "chocolate" ~ y_chocolate,
      exposure == "vanilla" ~ y_vanilla
    )
  )

data_observed |>
  group_by(exposure) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 2 × 2
  exposure  avg_outcome
  <chr>           <dbl>
1 chocolate        5.43
2 vanilla          4.33

So, what does it mean for exchangeability to be violated? Let’s say, instead, we allowed each participant to select their own ice cream flavor. 80% of the time, participants chose the flavor that made them happiest—their preference.

set.seed(11)
data_observed_exch <- data |>
  mutate(
    prefer_chocolate = y_chocolate > y_vanilla,
    exposure = case_when(
      # people who like chocolate more chose that 80% of the time
      prefer_chocolate ~ ifelse(
        rbinom(n(), 1, 0.8),
        "chocolate",
        "vanilla"
      ),
      # people who like vanilla more chose that 80% of the time
      !prefer_chocolate ~ ifelse(
        rbinom(n(), 1, 0.8),
        "vanilla",
        "chocolate"
      )
    ),
    observed_outcome = case_when(
      exposure == "chocolate" ~ y_chocolate,
      exposure == "vanilla" ~ y_vanilla
    )
  )

Now, it seems like vanilla makes you happier!

data_observed_exch |>
  group_by(exposure) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 2 × 2
  exposure  avg_outcome
  <chr>           <dbl>
1 chocolate        5.43
2 vanilla          5.67

Why does this happen? We’ll explore this problem more deeply in Chapter 4 and beyond, but from an assumptions perspective, exchangeability no longer holds. The potential outcomes are no longer the same on average for the two exposure groups. The average values for y(chocolate) are still pretty close, but y(vanilla) is quite different by group. The vanilla group no longer serves as a good proxy for this potential outcome for the chocolate group, and we get a biased result. What we see here is actually the potential outcomes for y(flavor, preference). This is always true because there are individuals for whom the individual causal effect is not 0. What’s changed is that the potential outcomes are no longer independent of which flavor a person has: their preference influences both the choice of flavor and the potential outcome. As we see in Figure 3.2, our groups are no longer exchangeable; they don’t have the same potential outcomes on average for y(vanilla).

data_observed_exch |>
  select(starts_with("y"), exposure) |>
  pivot_longer(
    starts_with("y"),
    names_prefix = "y_",
    names_to = "potential_outcome",
    values_to = "happiness"
  ) |>
  mutate(potential_outcome = paste0("y(", potential_outcome, ")")) |>
  ggplot(aes(happiness, exposure, color = exposure)) +
  geom_jitter(width = 0, height = .2, alpha = .5, color = "grey50") +
  stat_summary(fun = "mean", size = 2.5, geom = "point") +
  stat_summary(
    fun = "mean",
    geom = "text",
    aes(label = round(after_stat(x), 1)),
    vjust = -0.6,
    color = "black"
  ) +
  facet_wrap(~potential_outcome) +
  labs(y = "actual exposure", color = "actual\nexposure")

Figure 3.2: The average potential outcomes by observed exposure group in the presence of confounding. The groups are no longer exchangeable because the flavor assignment is no longer independent of the potential outcomes.

What can we do when exchangeability is violated? Throughout the book, we’ll devote a lot of time to this problem. The heart of the solution, though, is that we can sometimes still achieve exchangeability within levels of another variable. This is called conditional exchangeability: \(Y(x) \perp\!\!\!\perp X \mid Z\). In this case, we need exchangeability within levels of prefer_chocolate.

data_observed_exch |>
  mutate(prefer_chocolate = ifelse(
    prefer_chocolate,
    "prefers\nchocolate",
    "prefers\nvanilla"
  )) |>
  pivot_longer(
    starts_with("y"),
    names_prefix = "y_",
    names_to = "potential_outcome",
    values_to = "happiness"
  ) |>
  mutate(potential_outcome = paste0("y(", potential_outcome, ")")) |>
  ggplot(aes(happiness, exposure, color = exposure)) +
  geom_jitter(width = 0, height = .2, alpha = .5, color = "grey50") +
  stat_summary(fun = "mean", size = 2.5, geom = "point") +
  stat_summary(
    fun = "mean",
    geom = "text",
    aes(label = round(after_stat(x), 1)),
    vjust = -0.6,
    color = "black"
  ) +
  facet_grid(prefer_chocolate ~ potential_outcome) +
  labs(y = "actual exposure", color = "actual\nexposure")

Figure 3.3: The average potential outcomes by observed exposure group in the presence of confounding. We can still achieve conditional exchangeability within levels of the confounder. Here, we also start to see the limits of our sample size, as the potential outcomes, which would be valid in higher numbers, start to fail.

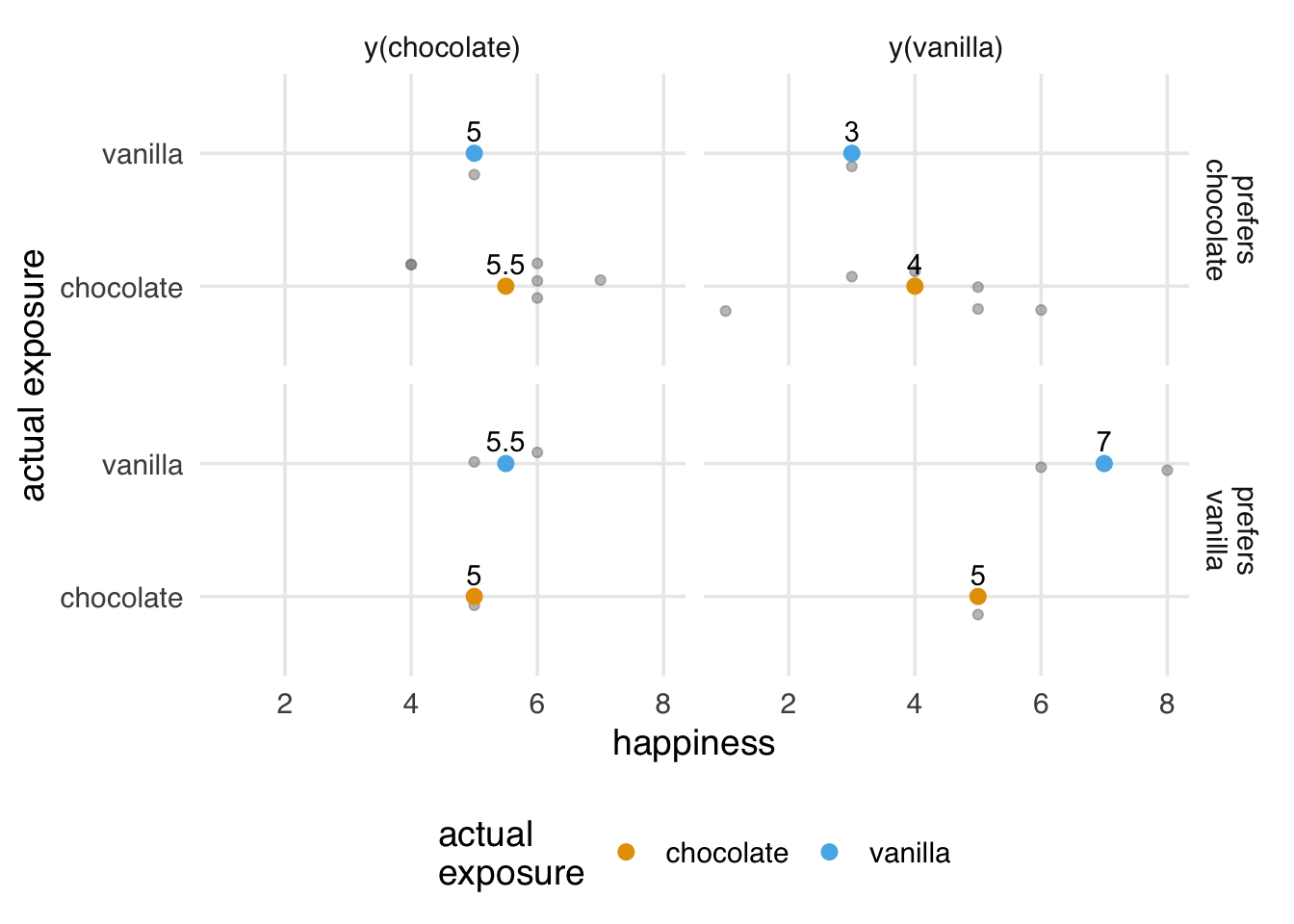
In Figure 3.3, we’ve already started to encounter the curse of dimensionality: our sample size is so small that we have very few values for the combination of exposure and preference. We’d achieve better exchangeability as our sample size increases, but this quickly becomes difficult without a good statistical model.

3.2.2 Positivity

The positivity assumption states that every individual has a non-zero probability of receiving each level of exposure. Mathematically, this means that \(P(X = x) > 0\) for all \(x\). In other words, we assume that there is no one for whom one or more levels of exposure are impossible. We need this assumption because it defines the potential outcome for a given exposure level. If someone is never, under any circumstances, exposed to chocolate, then the potential outcome for y(chocolate) isn’t defined for that person. We can’t use them to provide information about this potential outcome. In a randomized trial, the probability of exposure is known by design. In the ice cream example, everyone had the same probabilities: 50% to receive chocolate and 50% to receive vanilla. These possibilities define both potential outcomes for both groups.

Sometimes, positivity is referred to as the probabilistic assumption.

Positivity violations come in two forms: stochastic and structural. Stochastic violations are chance occurrences where you don’t have any observations for a given exposure level. In the example where 80% of participants chose the ice cream that would make them happiest, it’s feasible that, given our low sample size, we might end up with people who only choose chocolate. Naturally, we can only calculate the effect of vanilla vs. chocolate if we have observations of vanilla.

A nuance of positivity is that it needs to hold within levels of all covariates required for exchangeability: \(P(X = x \mid Z = z) > 0\) for all \(x\) and \(z\). Even if the flavors vary, we also need variability within levels of prefer_chocolate. That can also fail by chance.

set.seed(1)
data_observed_pos <- data |>
  mutate(
    prefer_chocolate = y_chocolate > y_vanilla,
    exposure = case_when(
      prefer_chocolate ~ ifelse(
        rbinom(n(), 1, 0.8),
        "chocolate",
        "vanilla"
      ),
      !prefer_chocolate ~ ifelse(
        rbinom(n(), 1, 0.8),
        "vanilla",
        "chocolate"
      )
    ),
    observed_outcome = case_when(
      exposure == "chocolate" ~ y_chocolate,
      exposure == "vanilla" ~ y_vanilla
    )
  )

data_observed_pos |>
  count(prefer_chocolate, exposure) |>
  complete(
    prefer_chocolate,
    exposure = c("chocolate", "vanilla"),
    fill = list(n = 0)
  )

# A tibble: 4 × 3
  prefer_chocolate exposure      n
  <lgl>            <chr>     <int>
1 FALSE            chocolate     0
2 FALSE            vanilla       3
3 TRUE             chocolate     7
4 TRUE             vanilla       0

Structural positivity violations are when an individual cannot receive at least one exposure level by definition. Let’s say some of our participants had an allergy to vanilla. Even in a randomized setting, these participants can’t eat vanilla. In this case, let’s say that anyone with an allergy to vanilla who is assigned vanilla switches to chocolate.

set.seed(11)
data_observed_struc <- data |>
  mutate(
    exposure = case_when(
      rbinom(n(), 1, 0.5) == 1 ~ "chocolate",
      TRUE ~ "vanilla"
    )
  )

set.seed(1)
data_observed_struc <- data_observed_struc |>
  mutate(
    # 30% chance of allergy
    allergy = rbinom(n(), 1, 0.3) == 1,
    # in which case `y_vanilla` is impossible
    exposure = ifelse(allergy, "chocolate", exposure),
    y_vanilla = ifelse(allergy, NA, y_vanilla),
    observed_outcome = case_when(
      # those with allergies always take chocolate
      allergy ~ y_chocolate,
      exposure == "chocolate" ~ y_chocolate,
      exposure == "vanilla" ~ y_vanilla
    )
  )

Now, our estimates are off quite a bit.

data_observed_struc |>
  group_by(exposure) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 2 × 2
  exposure  avg_outcome
  <chr>           <dbl>
1 chocolate         5.4
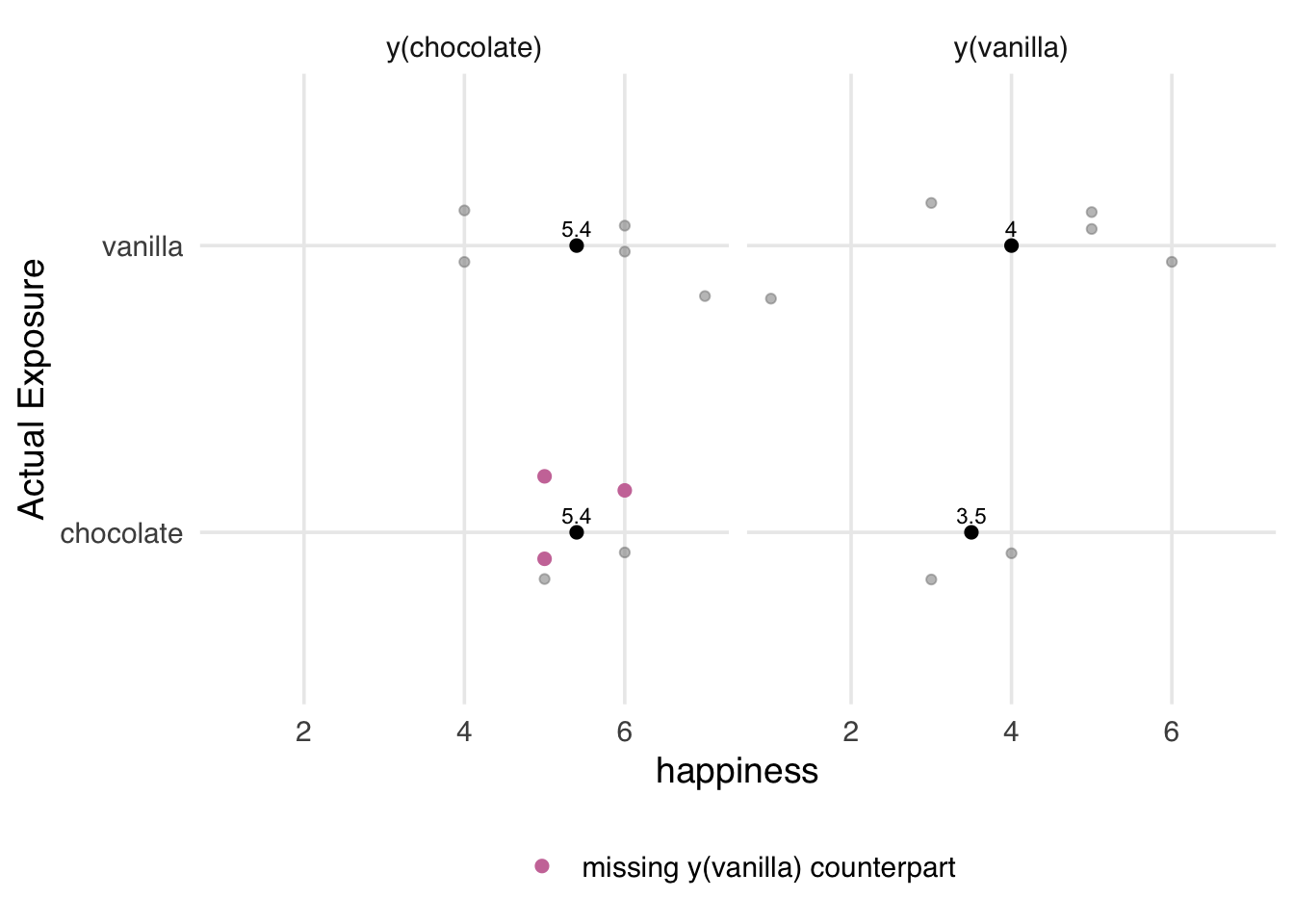
2 vanilla           4  

For those with a vanilla allergy, y_vanilla is not defined, as in Figure 3.4.

data_observed_struc |>
  mutate(is_missing_y_vanilla = is.na(y_vanilla)) |>
  select(starts_with("y"), exposure, is_missing_y_vanilla) |>
  pivot_longer(
    starts_with("y"),
    names_prefix = "y_",
    names_to = "potential_outcome",
    values_to = "happiness"
  ) |>
  mutate(
    potential_outcome = paste0("y(", potential_outcome, ")")
  ) |>
  ggplot(aes(happiness, exposure)) +
  geom_jitter(
    data = \(.x) filter(.x, !is_missing_y_vanilla),
    width = 0,
    height = .2,
    alpha = .5,
    color = "grey50"
  ) +
  geom_jitter(
    data = \(.x) filter(.x, is_missing_y_vanilla),
    aes(
      color = "missing y(vanilla) counterpart",
      fill = "missing y(vanilla) counterpart"
    ),
    size = 2,
    width = 0,
    height = .2,
    shape = 21
  ) +
  stat_summary(
    fun = "mean",
    geom = "text",
    aes(label = round(after_stat(x), 1)),
    vjust = -0.6,
    color = "black",
    size = 3
  ) +
  stat_summary(fun = "mean", size = 2, geom = "point") +
  facet_wrap(~potential_outcome) +
  labs(y = "Actual Exposure", color = NULL, fill = NULL) +
  ggokabeito::scale_color_okabe_ito(order = 7) +
  ggokabeito::scale_fill_okabe_ito(order = 7)

Figure 3.4: Potential outcomes in the presence of a structural positivity violation. When potential outcomes can’t occur, they are not defined. Those who have an allergy to vanilla do not have a counterpart y(vanilla).

There are a few things we can do to improve positivity problems. For stochastic positivity violations, we can collect more data. Increasing the sample size reduces the chances of stochastic violations. However, because we require positivity with each combination of covariates, we often need to use a statistical model to extrapolate over the data’s dimensionality. We’ll discuss this topic more in Chapter 8 and Chapter 13. Additionally, we can specify eligibility criteria (which we’ll discuss in Section 3.3.2) to exclude people for whom some level of exposure is impossible. If positivity is an issue within a particular confounder, we could also consider removing the confounder; if the confounding bias induced by not controlling for it is less than the bias induced by positivity, it might be worth the trade. Finally, we can modify the causal estimand we are trying to estimate. As we’ll see in Chapter 10, different causal effects are stricter in meeting the causal assumptions.

3.2.3 Consistency

Consistency assumes that the causal question you claim you are answering is consistent with the one you are actually answering with your analysis. Consistency allows us to see one of the potential outcomes for each group: the factual outcome. Mathematically, this means that \(Y_{obs} = (X)Y(1) + (1 - X)Y(0)\). In plain language, the consistency assumption says that the potential outcome of a given treatment value is equal to the value we actually observe when someone is assigned that treatment value. It seems almost silly when you say it. What else would it be? If you think this issue through, though, you’ll see that this assumption is violated nearly infinitely for any given exposure. Let’s consider two common cases:

• Poorly-defined exposure: For each exposure value, there is a difference between subjects when delivering that exposure. Put another way, multiple treatment versions exist. Instead, we need a well-defined exposure.
• Interference: The outcome (technically all potential outcomes, regardless of whether they are observed) for any subject depends on another subject’s exposure; Instead, we need no interference.

Consistency is sometimes called the stable-unit-treatment-value assumption or SUTVA (Imbens and Rubin 2015). However, causal consistency is a distinct idea from statistical consistency, which is a property where an estimator moves closer to the truth as the sample size increases.

3.2.3.1 Poorly-defined exposures

Consistency violations are common when an exposure is poorly defined. They occur in everything from surgeries (say if one doctor is more experienced with a surgical procedure than another) to income (are all income sources dollar-for-dollar the same? Is the lottery the same as a weekly paycheck?) to education (do years of education have the same effect across school quality?), and many others (Rehkopf, Glymour, and Osypuk 2016).

Suppose there were two containers of chocolate ice cream, one of which was spoiled. Exposure to “chocolate” could mean different things depending on where the individual’s scoop came from (regular chocolate ice cream or spoiled chocolate ice cream); we are lumping them all together under a single term. Eating spoiled ice cream makes you miserable, regardless of how you feel about chocolate ice cream in general, so it is not the same potential outcome.

data <- tibble(
  id = 1:10,
  y_spoiled_chocolate = c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
  y_chocolate = c(4, 4, 6, 5, 6, 5, 6, 7, 5, 6),
  y_vanilla = c(1, 3, 4, 5, 5, 6, 8, 6, 3, 5)
) |>
  mutate(causal_effect = y_chocolate - y_vanilla)

set.seed(11)
data_observed_poorly_defined <- data |>
  mutate(
    exposure_unobserved = case_when(
      rbinom(n(), 1, 0.25) == 1 ~ "chocolate (spoiled)",
      rbinom(n(), 1, 0.25) == 1 ~ "chocolate",
      TRUE ~ "vanilla"
    ),
    observed_outcome = case_match(
      exposure_unobserved,
      "chocolate (spoiled)" ~ y_spoiled_chocolate,
      "chocolate" ~ y_chocolate,
      "vanilla" ~ y_vanilla
    ),
    exposure = case_match(
      exposure_unobserved,
      c("chocolate (spoiled)", "chocolate") ~ "chocolate",
      "vanilla" ~ "vanilla"
    )
  )

We know the true average causal effect of (unspoiled) chocolate in the sample is 0.8; however, our estimated causal effect is 1.1.

data_observed_poorly_defined |>
  group_by(exposure) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 2 × 2
  exposure  avg_outcome
  <chr>           <dbl>
1 chocolate        2.75
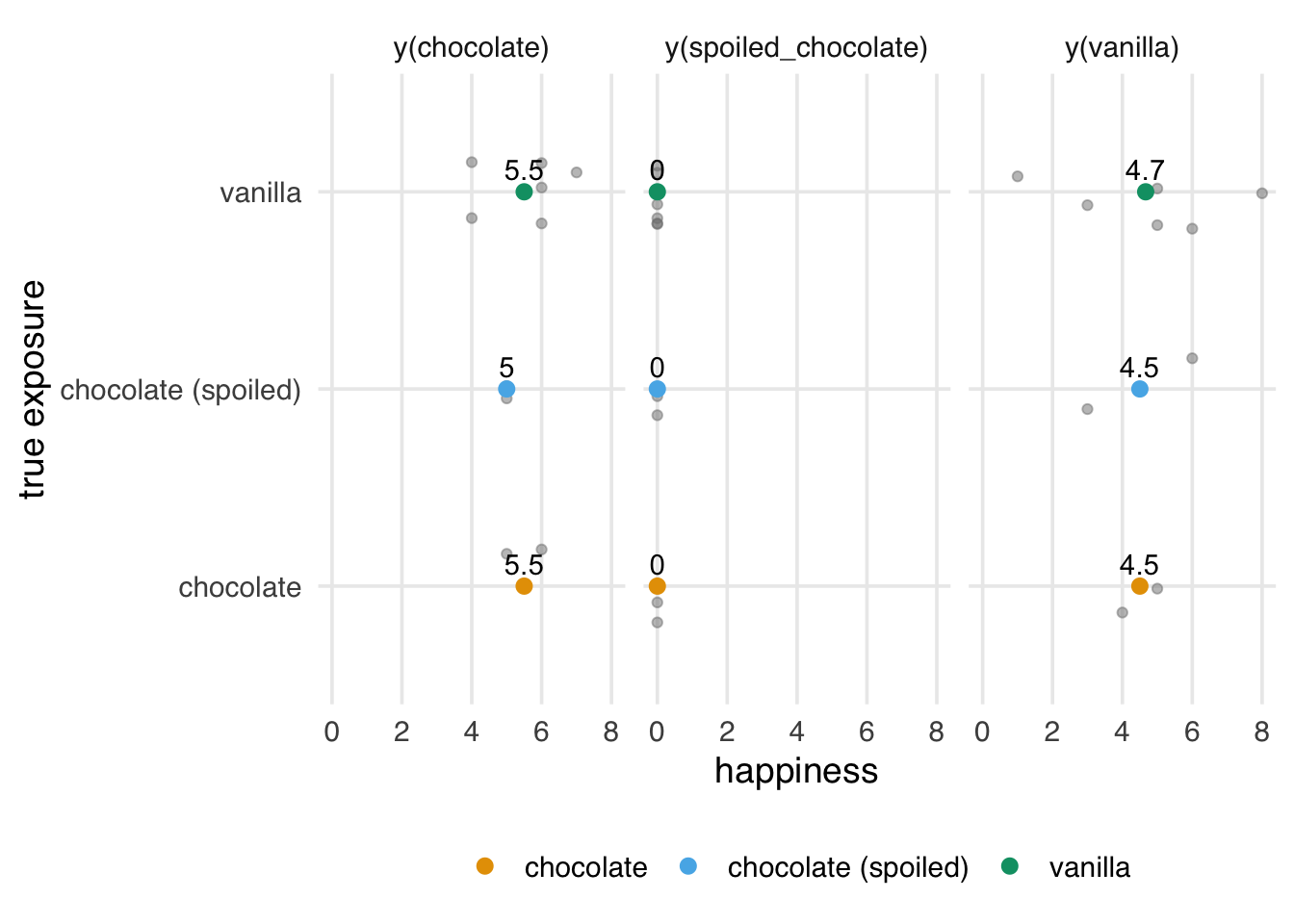
2 vanilla          4.67

The potential outcome we think we are estimating is not the one we are observing. We’re treating fresh chocolate ice cream and spoiled chocolate ice cream as the same exposure, but they have different effects on the potential outcomes. Because the exposure is random, we actually do a pretty good job of estimating the effect of y(chocolate, spoiled = FALSE) | y(chocolate, spoiled = TRUE), but that’s not what we’re interested in. We just want y(chocolate, spoiled = FALSE).

data_observed_poorly_defined |>
  mutate(
    is_spoiled = exposure_unobserved == "chocolate (spoiled)"
  ) |>
  pivot_longer(
    cols = starts_with("y"),
    names_prefix = "y_",
    names_to = "potential_outcome",
    values_to = "happiness"
  ) |>
  mutate(
    potential_outcome = case_when(
      potential_outcome == "spoiled_chocolate" ~ "chocolate",
      TRUE ~ potential_outcome
    ),
    potential_outcome = paste0("y(", potential_outcome, ")")
  ) |>
  ggplot(aes(happiness, exposure)) +
  geom_jitter(
    data = \(.x) filter(.x, !(potential_outcome == "y(chocolate)" & exposure == "chocolate")),
    width = 0,
    height = 0.2,
    alpha = 0.5,
    color = "grey50"
  ) +
  geom_jitter(
    data = \(.x) filter(.x, potential_outcome == "y(chocolate)" & exposure == "chocolate"),
    aes(color = is_spoiled, fill = is_spoiled),
    size = 2,
    width = 0,
    height = 0.2,
    alpha = 0.8,
    shape = 21
  ) +
  stat_summary(
    fun = "mean",
    size = 2,
    geom = "point"
  ) +
  stat_summary(
    fun = "mean",
    geom = "text",
    aes(label = round(after_stat(x), 1)),
    vjust = -0.6,
    color = "black",
    size = 3
  ) +
  facet_wrap(~potential_outcome) +
  labs(
    y = "actual exposure",
    color = "spoiled",
    fill = "spoiled"
  )

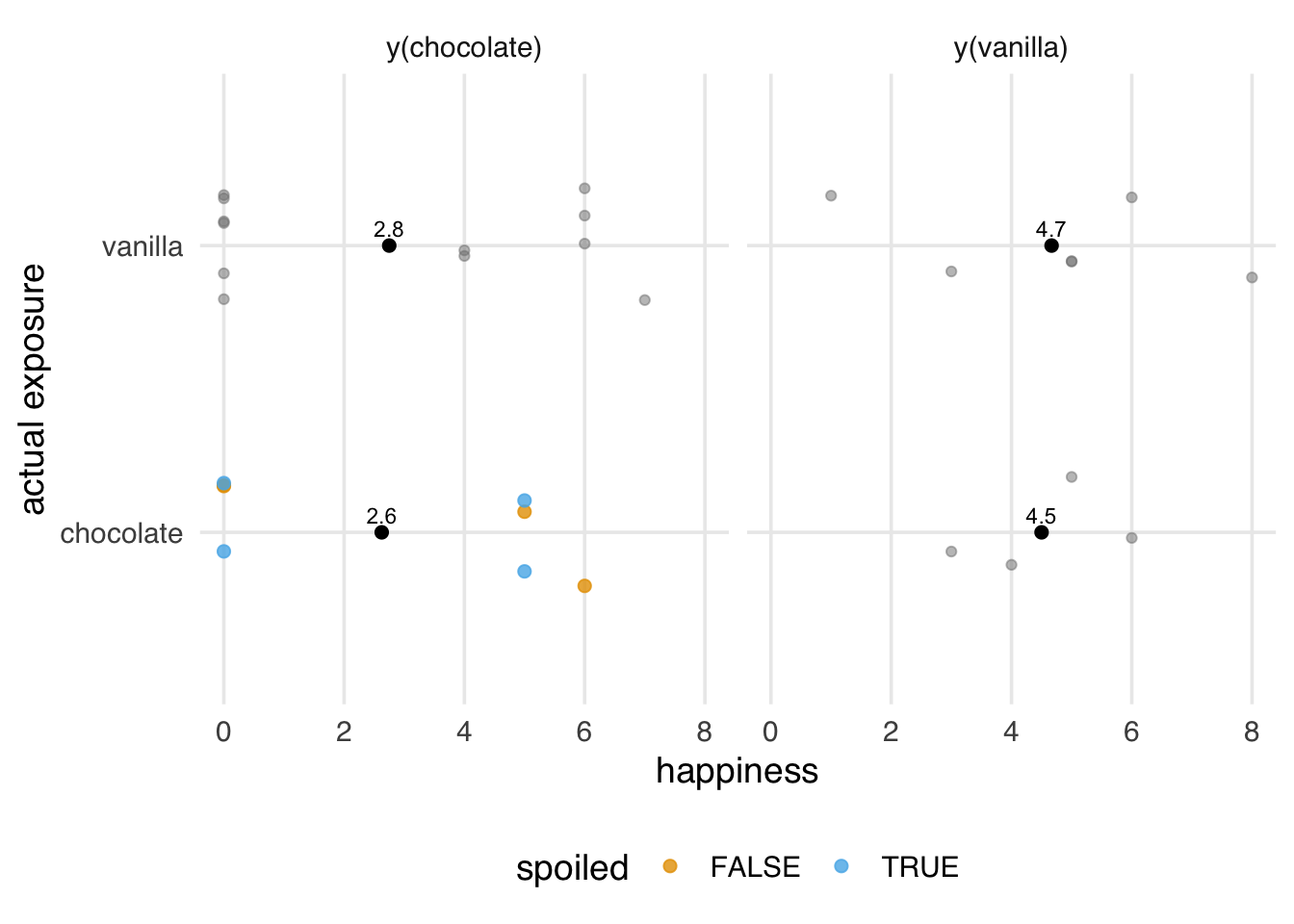
Figure 3.5: Potential outcomes under a consistency violation. Consistency allows us to treat the observed data as the factual outcome. Here, we’re treating the chocolate group as representative of y(chocolate), but this isn’t true. The data represent a mixture of y(chocolate, spoiled = FALSE) and y(chocolate, spoiled = TRUE), different potential outcomes.

We can imagine other ways in which slight variations in the treatment occur: high-quality and low-quality brands of vanilla ice cream are categorized as “vanilla.” One person eats in the morning and another in the afternoon. One has a spoonful, and one has three bowls full. There will almost always be some consistency violation in this sense; the question for us is whether or not that violation is meaningful regarding the potential outcomes we see. If two brands of ice cream produce the same happiness, this variation doesn’t matter. If they differ, by how much?

One way to address consistency violations, in addition to being more specific, is to investigate potential deviations within treatment levels. Let’s say we tested the ice cream containers after the experiment and had data on the spoiled status of the ice cream in the data. Now, we can group it by the actual exposure.

data_observed_poorly_defined |>
  group_by(exposure_unobserved) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 3 × 2
  exposure_unobserved avg_outcome
  <chr>                     <dbl>
1 chocolate                  5.5 
2 chocolate (spoiled)        0   
3 vanilla                    4.67

Now we’re back to the right answer because we’ve correctly separated the potential outcomes in our analysis, as in Figure 3.6.

data_observed_poorly_defined |>
  pivot_longer(
    starts_with("y"),
    names_prefix = "y_",
    names_to = "potential_outcome",
    values_to = "happiness"
  ) |>
  mutate(potential_outcome = paste0("y(", potential_outcome, ")")) |>
  ggplot(aes(happiness, exposure_unobserved, color = exposure_unobserved)) +
  geom_jitter(width = 0, height = .2, alpha = .5, color = "grey50") +
  stat_summary(fun = "mean", size = 2.5, geom = "point") +
  stat_summary(
    fun = "mean",
    geom = "text",
    aes(label = round(after_stat(x), 1)),
    vjust = -0.6,
    color = "black"
  ) +
  facet_wrap(~potential_outcome) +
  labs(y = "true exposure", color = NULL)

Figure 3.6: Potential outcomes under a consistency violation. Now we’ve correctly linked the observed data to their underlying potential outcome, making them consistent.

3.2.3.2 Interference

Interference means that an individual’s exposure impacts another’s potential outcome. It’s very common in infectious diseases, where someone’s exposure to a vaccine or treatment often impacts someone else’s outcome risk. However, it can also occur in various other settings, including via social networks, policy interventions, the geographic proximity of treated units, and so on.

Let’s say each individual in our ice cream study has a partner, and their potential outcome depends on both what flavor of ice cream they ate and what flavor their partner ate. In the simulation below, having a partner who receives a different flavor of ice cream increases their happiness by two units.

data <- tibble(
  id = 1:10,
  partner_id = c(1, 1, 2, 2, 3, 3, 4, 4, 5, 5),
  y_chocolate_chocolate = c(4, 4, 6, 5, 6, 5, 6, 7, 5, 6),
  y_vanilla_vanilla = c(1, 3, 4, 5, 5, 6, 8, 6, 3, 5)
) |>
  # partner's happiness increases by 2
  # when they get a different flavor
  mutate(
    y_chocolate_vanilla = y_chocolate_chocolate + 2,
    y_vanilla_chocolate = y_vanilla_vanilla + 2
  )

set.seed(37)
data_observed_interf <- data |>
  mutate(
    exposure = case_when(
      rbinom(n(), 1, 0.5) == 1 ~ "chocolate",
      TRUE ~ "vanilla"
    ),
    exposure_partner = case_when(
      rbinom(n(), 1, 0.5) == 1 ~ "chocolate",
      TRUE ~ "vanilla"
    ),
    observed_outcome = case_when(
      exposure == "chocolate" & exposure_partner == "chocolate" ~
        y_chocolate_chocolate,
      exposure == "chocolate" & exposure_partner == "vanilla" ~
        y_chocolate_vanilla,
      exposure == "vanilla" & exposure_partner == "chocolate" ~
        y_vanilla_chocolate,
      exposure == "vanilla" & exposure_partner == "vanilla" ~
        y_vanilla_vanilla
    )
  )

As with a poorly defined exposure, we don’t get the right answer under interference.

data_observed_interf |>
  group_by(exposure) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 2 × 2
  exposure  avg_outcome
  <chr>           <dbl>
1 chocolate        6.25
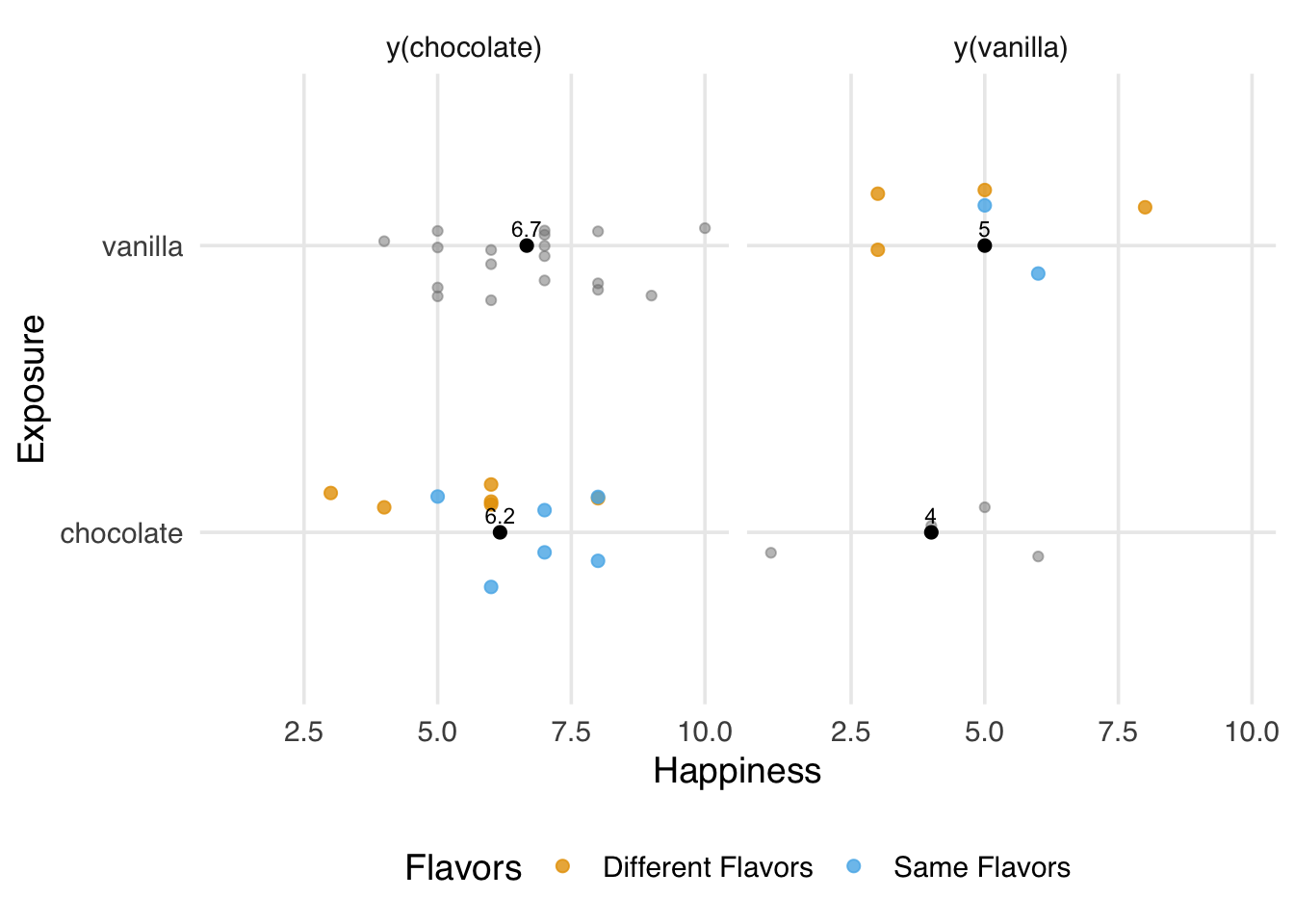
2 vanilla          6.33

Similarly, the problem is that we’re estimating the wrong potential outcome (Figure 3.7). Interference and poorly defined exposures are different manifestations of the same assumption violation. The potential outcomes we are estimating are not consistent with the causal question we’re asking.

data_observed_interf |>
  pivot_longer(
    cols = starts_with("y_"),
    names_prefix = "y_",
    names_to = "potential_outcome",
    values_to = "happiness"
  ) |>
  mutate(
    potential_outcome = case_when(
      grepl("chocolate", potential_outcome) ~ "y(chocolate)",
      grepl("vanilla", potential_outcome) ~ "y(vanilla)"
    ),
    observed = case_when(
      potential_outcome == "y(chocolate)" & exposure == "chocolate" ~ TRUE,
      potential_outcome == "y(vanilla)" & exposure == "vanilla" ~ TRUE,
      TRUE ~ FALSE
    ),
    flavor_match = ifelse(exposure == exposure_partner, "Same Flavors", "Different Flavors") # Collapse to same/different
  ) |>
  ggplot(aes(happiness, exposure)) +
  geom_jitter(
    data = \(.x) filter(.x, !observed),
    width = 0,
    height = 0.2,
    alpha = 0.5,
    color = "grey50"
  ) +
  geom_jitter(
    data = \(.x) filter(.x, observed),
    aes(color = flavor_match, fill = flavor_match),
    size = 2,
    width = 0,
    height = 0.2,
    alpha = 0.8,
    shape = 21
  ) +
  stat_summary(
    fun = "mean",
    size = 2,
    geom = "point",
    color = "black"
  ) +
  stat_summary(
    fun = "mean",
    geom = "text",
    aes(label = round(after_stat(x), 1)),
    vjust = -0.6,
    color = "black",
    size = 3
  ) +
  facet_wrap(~potential_outcome) +
  labs(
    y = "Exposure",
    x = "Happiness",
    color = "Flavors",
    fill = "Flavors"
  )

Figure 3.7: Potential outcomes under a consistency violation. This time, the vanilla group’s y(vanilla) and the chocolate group’s y(chocolate) are not correct: they are a mixture of effects due to interference by the partner’s flavor.

As before, we can be more specific about the potential outcomes.

data_observed_interf |>
  group_by(exposure, exposure_partner) |>
  summarise(avg_outcome = mean(observed_outcome), .groups = "drop")

# A tibble: 4 × 3
  exposure  exposure_partner avg_outcome
  <chr>     <chr>                  <dbl>
1 chocolate chocolate               5.5 
2 chocolate vanilla                 7   
3 vanilla   chocolate               6.75
4 vanilla   vanilla                 5.5 

One of the main ways to combat interference is to change the unit under consideration. Here, each individual, each unique ID, is considered a unit, and there is interference between units (i.e., partners). Suppose we consider each partnership as a unit and randomize the partnerships rather than the individuals. In that case, we solve the interference issue, as there is no interference between different partner sets. This type of randomization is sometimes referred to as a cluster randomized trial. What we decide to do within each cluster may depend on the causal question at hand. For example, if we want to know what would happen if both people ate chocolate ice cream versus vanilla ice cream, we would want to randomly assign both partners to either chocolate or vanilla, as seen below.

set.seed(11)

## we are now randomizing the *partnerships* not the individuals
partners <- tibble(
  partner_id = 1:5,
  exposure = case_when(
    rbinom(5, 1, 0.5) == 1 ~ "chocolate",
    TRUE ~ "vanilla"
  )
)
partners_observed <- data |>
  left_join(partners, by = "partner_id") |>
  mutate(
    # all partnerships have the same exposure
    exposure_partner = exposure,
    observed_outcome = case_when(
      exposure == "chocolate" & exposure_partner == "chocolate" ~
        y_chocolate_chocolate,
      exposure == "vanilla" & exposure_partner == "vanilla" ~
        y_vanilla_vanilla
    )
  )

Now, we can detect the correct causal effect.

partners_observed |>
  group_by(exposure) |>
  summarise(avg_outcome = mean(observed_outcome))

# A tibble: 2 × 2
  exposure  avg_outcome
  <chr>           <dbl>
1 chocolate        5.5 
2 vanilla          4.38

There are also methods for identifying effects with multiple versions of treatments or interference, but they are technical and more limited under their consistency violations (Tchetgen and VanderWeele 2010; VanderWeele and Hernan 2013).

Similarly, we could assign partners either the same flavor or different flavors, which would allow us to calculate the cross-flavor effect. Another option would be to exclude partners so there is no interference effect. The key is to think about what you want to estimate and try to represent the potential outcomes for that question as precisely as possible.

Malaria nets, revisited

In Chapter 2, we estimated the causal effect of mosquito nets on malaria risk. Let’s consider the causal assumptions for this question and how they might have been violated in a real-life analysis.

• Exchangeability: We saw what can happen with this problem when an unmeasured confounder (in this case, genetic resistance to malaria) is present. Thinking about exchangeability is one of the more demanding and more common tasks in causal inference with observational data. We’ll discuss this in-depth in Chapter 4, and what to do if we think (or know) we’re wrong in Chapter 16. We should also be concerned that we haven’t measured the covariates we need well or are missing values (Chapter 15).
• Positivity: A positivity violation would occur if any household would always or never use a bed net. A situation like this is feasible in real life. Someone may be allergic to the material, or one type of net may be unapproved in a region. As mentioned, we also need positivity to hold within the levels of the combination confounders in the analysis. Is it possible, for instance, that someone of low economic status in cold weather (when mosquitoes are not very active) and good health would never use a bed net because it wasn’t worth the expense?
• Consistency: We already saw an example of the well-defined exposure problem: a “bed net” can mean many things. We decided we were comparing insecticide-treated bed nets compared to no nets, but we may need more. Does the manufacturer matter? The type of insecticide? The amount of insecticide? We need to think about the effect on the potential outcomes each of these variations might have. Interference is a real problem for bed-net research, particularly for insecticidal nets. Notably, we used households as the unit of observation, which would reduce some of the local interference. We could also consider households that are geographically dispersed from one another.

3.3 When do study designs support causal inference?

Exchangeability, positivity, and consistency are simple assumptions, but as we’ve seen, they can easily be violated. When the assumptions for a causal method are not met, we cannot use the observed data to simulate counterfactuals and compare them to the observed outcomes. However, we can address many of the potential violations through careful study design, whether before collecting data or working with “found” observational data.

3.3.1 Randomized trials

As we’ve seen, randomized trials have excellent properties in terms of meeting the causal assumptions we need. In the limit, we expect exchangeability because the only cause of the exposure is the randomization process itself. Since it’s random, it’s completely independent of the potential outcomes under study. Similarly, the randomization process guarantees positivity so long as no one has a deterministic exposure; we know the probabilities we use to assign exposures. Randomized trials also help, but do not guarantee, consistency, particularly for well-defined exposures. An exposure needs to be defined in order to be administered. Interference, however, can still happen. For instance, if we randomize some people to receive a vaccine for an infectious disease, their receiving it could lower the chance of those around them contracting it because it changes the probability of exposure. This requires additional considerations in the trial’s design, e.g., cluster randomization or unit separation, as in the examples above.

We refer to analyses where the exposure is randomly assigned as a randomized trial. Sometimes, this type of randomized design is called an A/B test, as in “Which is better, A or B?”. A/B tests are common in industry, for instance, in testing two different website UI designs. At their heart, though, they are randomized experiments, and everything in this section still applies.

However, these properties are for an ideal randomized trial. In actual randomized trials, things can go wrong. Exchangeability can fail by chance when the sample size is too low. People also don’t necessarily do what they’re told to do; many people in studies will not adhere to their assigned exposure. Often, the reasons for non-adherence create problems of exchangeability. Similarly, people may drop out of a study in a way that creates non-exchangeability. We’ll tackle these topics and what we can do about them in more depth in Chapter 18 and Chapter 22. Exposures can also be inconsistent in real trials, either by implementation (as in the surgery example above) or by participants. For instance, a participant might be assigned to take two pills per day but decide to only take one per day. Attempts to prevent interference can also fail, e.g., randomizing on the wrong unit or units interacting with one another unexpectedly.

Non-randomized (observational) studies have none of these guarantees, even ideal ones. Like a realistic randomized trial, observational studies require careful design and execution to better meet the assumptions necessary for causal inference. Table 3.4 summarizes how well ideal randomized trials, realistic randomized trials, and observational studies each meet the exchangeability, positivity, and consistency criteria.

Assumption	Ideal Randomized Trial	Realistic Randomized Trial	Observational Study
Consistency (Well defined exposure)	😄	🤷	🤷
Consistency (No interference)	🤷	🤷	🤷
Positivity	😄	😄	🤷
Exchangeability	😄	🤷	🤷

Table 3.4: Assumptions solved by study design. 😄 indicates it is solved by default, 🤷 indicates that it is solvable but not solved by default.

The design of a causal analysis requires a clear causal question. We then can map this question to a protocol, consisting of the following seven elements, as defined by Hernán and Robins (2016):

• Eligibility criteria: Who or what should be included in the study?
• Exposure definition: When eligible, what precise exposure will units under study receive?
• Assignment procedures: How will eligible units be assigned to an exposure?
• Follow-up period: When does follow-up start and end?
• Outcome definition: What precise outcomes will be measured?
• Causal contrast of interest: Which causal estimand will be estimated?
• Analysis plan: What data manipulation and statistical procedures will be applied to the data to estimate the causal contrast of interest?

Recall our diagrams from Section 1.3 (Figure 1.6); several of these protocol elements can be mapped to these diagrams when we are attempting to define our causal question.

Figure 3.8: Example diagram mapped to causal analysis terminology

3.3.2 Emulating target trials

Randomized trials help meet the causal assumptions, but as discussed in Chapter 1, there are many reasons we may not be able to randomize, including time, money, and ethical considerations. We might also be able to get a preliminary answer sooner with observational data while randomized trials are being conducted.

Even when we are not conducting a randomized trial, imagining how such a trial would proceed can improve the quality of inferences from observational data. This is the idea behind target trial emulation: you specify a target trial (the randomized trial you would run or which has been run previously) and try to emulate this design with observational data.

Whether the design is a randomized trial or observational study, using a protocol can improve our likelihood of meeting the causal assumptions. In Table 3.5, we map these elements to the corresponding assumption they can address.

Assumption	Eligibility Criteria	Exposure Definition	Assignment Procedures	Follow-up Period	Outcome Definition	Causal contrast	Analysis Plan
Consistency (Well-defined exposure)	✔️	✔️	✔️				✔️
Consistency (No interference)	✔️	✔️	✔️		✔️		✔️
Positivity	✔️	✔️	✔️			✔️	✔️
Exchangeability	✔️	✔️	✔️	✔️	✔️	✔️	✔️

Table 3.5: Mapping assumptions to elements of a study protocol

• Eligibility criteria: Eligibility criteria are beneficial for preventing positivity violations (by excluding those who can never have one of the exposures) but are also helpful for consistency and exchangeability. You can, for instance, exclude people who are likely to affect each other’s outcomes or only include people without extreme characteristics.
• Exposure definition: A precise exposure definition is particularly useful for improving consistency since it encourages a well-defined exposure and can better control the potential of interference. A precise exposure also helps identify factors related to exchangeability and positivity.
• Assignment procedures: In randomized assignment, exchangeability and positivity are met. Understanding how an exposure occurs also improves exchangeability and positivity in non-randomized studies. As we’ve seen, we can also use assignment procedures to prevent interference, and likewise, they can help improve a well-defined exposure since the assignment mechanism needs to be precise.
• Follow-up period: We’ll discuss the issues that defining a follow-up period solves in more detail in Chapter 18, but it helps with exchangeability by ensuring the follow-up time is comparable for all exposure levels. It’s also closely related to consistency because a well-defined exposure may require a time element.
• Outcome definition: Precisely defining the outcome helps identify prognostic factors, improving precision in a randomized trial but also improving exchangeability in an observational study.
• Causal contrast of interest: As we’ll see in Chapter 10, some causal contrasts are less strict about exchangeability and positivity than others.
• Analysis plan: A clear analysis plan improves all aspects of meeting the causal assumptions in observational studies. For instance, we must be clear about variables we must adjust to meet exchangeability. Additionally, while we can never confirm the assumptions of a causal method are met, we can provide evidence through exploratory analysis (Chapter 7) or probe the consequences of violating them with sensitivity analysis (Chapter 16).

What would a target trial and emulation look like for the ice cream example? Imagine that we have a database that has all the information we need. A store serves precisely 100g of either chocolate or vanilla, both of the same brand. Thanks to this database, we have information on participants’ flavor choices and a variety of other characteristics, including happiness (measured by the same tool we used above), with measurements at the door (baseline) and 30 minutes after eating their ice cream (follow-up). In Table 3.6, we outline some ideas for a randomized trial of this question and an observational study that would emulate it using this database. Notably, the target trial we can emulate is usually a so-called pragmatic trial—a trial without blinding. That is because it’s often not possible to blind someone’s exposure from themselves.

Protocol Step	Description	Target Trial	Emulation
Eligibility criteria	Who should be included in the study?	Inclusion: Age 18 to 65. Exclusion: No lactose intolerance or allergy to any ingredients; entered store within the week of the study.	Same as target trial.
Exposure definition	When eligible, what precise exposure will units under study receive?	100g vanilla or chocolate ice cream in a bowl, both Don and Jerzy brand ice cream.	Same as target trial.
Assignment procedures	How will eligible units be assigned to an exposure?	Participants are randomized with a 50% probability of either flavor. The assignment is non-blinded.	Participants are assigned the flavor consistent with their data, e.g., the flavor they chose. Randomization is emulated using baseline covariates.
Follow-up period	When does follow-up start and end?	Start: When eligibility criteria are met and flavor is assigned; End: 30 minutes after flavor assignment.	Same as target trial.
Outcome definition	What precise outcomes will be measured?	Happiness (1-10) as measured by the gold-standard tool.	Same as target trial.
Causal contrast of interest	Which causal estimand will be estimated?	Average Treatment Effect (ATE).	Same as target trial.
Analysis plan	What data manipulation and statistical procedures will be applied to the data to estimate the causal contrast of interest?	ATE will be calculated using inverse probability weighting, weighted for baseline happiness, age, income, education, physical activity, self-rated physical health, self-rated mental health, quality of relationships, and preference of flavor.	ATE will be calculated using inverse probability weighting, weighted for confounders (baseline happiness, age, preference of flavor) and additional baseline prognostic variables (age, income, education, physical activity, self-rated physical health, self-rated mental health, and quality of relationships).

Table 3.6: A protocol of a target trial of ice cream flavor on happiness and a corresponding protocol for an observational study that emulates the target trial

The protocol in Table 3.6 helps us meet the causal assumptions in a variety of ways. For instance, we are more likely to have positivity without people with allergies or sensitivities. We’re more likely to have consistency when the exposure is well-defined. If we thought interference was an issue, we could also change the randomization procedure to use a cluster design or exclude people we think might interfere with one another (for instance, by only including one person per group). We also try to address exchangeability by replicating randomization through IPW. In this causal question, we believe that mutual causes of flavor choice and happiness are baseline happiness, age, and preference of flavor. We think additional causes of happiness are age, income, education, physical activity, self-rated physical health, self-rated mental health, and quality of relationships. We’ll discuss this idea in greater detail in Chapter 4. There are a few other elements here that we’ll take up in more detail later. As mentioned, we’ll address follow-up in Chapter 18 and estimands in Chapter 10, including estimands that are specific to randomized trials. We also use IPW for the target trial even though we are randomizing. We’ll discuss the benefits of this in Section 6.3.1.

Century, D. 2022. Split Decision: Life Stories. Gallery Books. https://books.google.com/books?id=bN9IEAAAQBAJ.

Hernán, Miguel A, and James M Robins. 2016. “Using Big Data to Emulate a Target Trial When a Randomized Trial Is Not Available.” American Journal of Epidemiology 183 (8): 758–64.

Imbens, Guido W, and Donald B Rubin. 2015. Causal Inference in Statistics, Social, and Biomedical Sciences. Cambridge University Press.

Rehkopf, David H., M. Maria Glymour, and Theresa L. Osypuk. 2016. “The Consistency Assumption for Causal Inference in Social Epidemiology: When a Rose Is Not a Rose.” Current Epidemiology Reports 3 (1): 63–71. https://doi.org/10.1007/s40471-016-0069-5.

Tchetgen, Eric J Tchetgen, and Tyler J VanderWeele. 2010. “On Causal Inference in the Presence of Interference.” Statistical Methods in Medical Research 21 (1): 55–75. https://doi.org/10.1177/0962280210386779.

VanderWeele, Tyler J., and Miguel A. Hernan. 2013. “Causal Inference Under Multiple Versions of Treatment.” Journal of Causal Inference 1 (1): 1–20. https://doi.org/10.1515/jci-2012-0002.

---

1. Ice cream swirls were prohibited per the study protocol.

2. These causal assumptions are in addition to any statistical assumptions, such as distributional assumptions, that the estimators we use require.

3. The numbers are slightly different because of the sample size. As the sample size increases, exchangeability is more likely to hold with randomization, and so with a large enough sample, we’d get identical answers.