You are reading the work-in-progress first edition of Causal Inference in R. This chapter is mostly complete, but we might make small tweaks or copyedits.
6 From question to answer: stratification and outcome models
Let’s finally turn our attention to methods for answering causal questions, the subject of most of the rest of the book. Potential outcomes, counterfactuals, and DAGs allow us to establish the conditions under which we can estimate causal effects. Now, we need tools to estimate them. This chapter is a transition point as we explore models to make causal inference more feasible.
But let’s begin with no model at all.
6.1 Causal inference with group_by() and summarize()
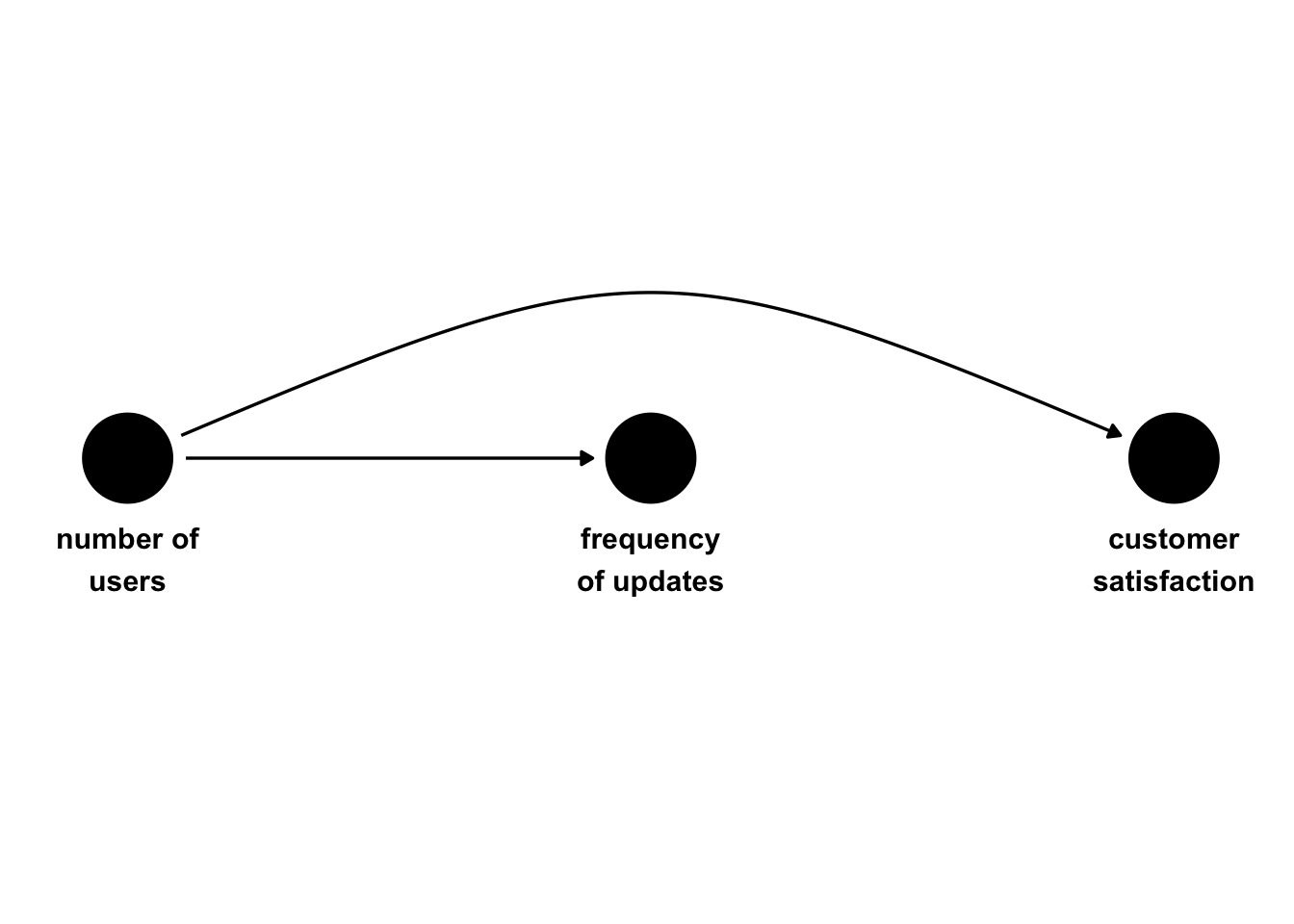
Let’s suppose we are analyzing data from a company that creates software. We are trying to estimate the causal effect of software update frequency on customer satisfaction (measured as a standardized score with a population mean of 0 and standard deviation of 1). The customers are organizations that have individual users, and the organization as a whole receives either weekly or daily updates. Update frequency is not randomized, and, as shown in Figure 6.1, the exposure and outcome have a mutual cause—a confounder—customer type. Free customers are more likely to receive weekly updates, while premium customers are more likely to receive daily updates. Premium customers are more likely to have higher satisfaction. Even though there is no relationship between the exposure and outcome, we expect confounding from the open backdoor path between updates and satisfaction via customer_type. We have confounding by a single binary confounder.
Code
library(ggdag)
coords1 <- list(
x = c(customer_type = 1, updates = 2, satisfaction = 3),
y = c(customer_type = 0, updates = 0, satisfaction = 0)
)
dag1 <- dagify(
satisfaction ~ customer_type,
updates ~ customer_type,
coords = coords1,
labels = c(
customer_type = "customer type",
updates = "frequency\nof updates",
satisfaction = "customer\nsatisfaction"
)
)
ggdag(dag1, use_text = FALSE, use_edges = FALSE) +
geom_dag_text(aes(label = label), nudge_y = c(-.05, -.05, -.05), color = "black") +
geom_dag_edges_arc(curvature = c(0.07, 0)) +
theme_dag() +
ylim(c(.2, -.2))Let’s simulate some data that matches this data-generating process. In this simulation, we generate the potential outcomes for satisfaction(weekly) and satisfaction(daily). Many of the simulations in this book skip this step and simulate the observed outcomes directly; however, as we transition into answering causal questions, it’s helpful to remember what assumptions we need to meet in order to make inferences.
set.seed(1)
n <- 10000
satisfaction1 <- tibble(
# Free (0) or Premium (1)
customer_type = rbinom(n, 1, 0.5),
p_exposure = case_when(
# Premium customers are more likely to receive daily updates
customer_type == 1 ~ 0.75,
# Free customers are more likely to receive weekly updates
customer_type == 0 ~ 0.25
),
# Weekly (0) vs Daily (1)
update_frequency = rbinom(n, 1, p_exposure),
# generate the "true" average treatment effect of 0
# to do this, we are going to generate the
# potential outcomes, first if exposure = 0
# `y0` = `satisfaction(weekly)`
# notice `update_frequency` is not in the equation below
# we use rnorm(n) to add the random error term that is normally
# distributed with a mean of 0 and a standard deviation of 1
y0 = customer_type + rnorm(n),
# because the true effect is 0, the potential outcome
# if exposure = 1 is identical
y1 = y0,
# in practice, we will only see one of these
# observed
satisfaction = (1 - update_frequency) * y0 +
update_frequency * y1,
observed_potential_outcome = case_when(
update_frequency == 0 ~ "y0",
update_frequency == 1 ~ "y1"
)
) |>
mutate(
satisfaction = as.numeric(scale(satisfaction)),
update_frequency = factor(
update_frequency,
labels = c("weekly", "daily")
),
customer_type = factor(
customer_type,
labels = c("free", "premium")
)
)satisfaction1 |>
select(update_frequency, customer_type, satisfaction)# A tibble: 10,000 × 3
update_frequency customer_type satisfaction
<fct> <fct> <dbl>
1 weekly free -1.16
2 weekly free -1.39
3 daily premium -0.473
4 daily premium -0.608
5 weekly free -0.891
6 daily premium -0.0145
7 weekly premium 0.185
8 weekly premium 0.881
9 weekly premium 0.234
10 weekly free 0.690
# ℹ 9,990 more rowsNow, let’s try to estimate the effect of the update_frequency on the satisfaction, assuming the two exposed groups are exchangeable.
satisfaction1 |>
group_by(update_frequency) |>
summarise(avg_satisfaction = mean(satisfaction))# A tibble: 2 × 2
update_frequency avg_satisfaction
<fct> <dbl>
1 weekly -0.237
2 daily 0.238Of course, from the DAG and how we simulated the potential outcomes, we know that the two groups are not exchangeable. The true difference between the update frequency groups is 0, but there is a difference in average satisfaction between them. As discussed in Chapter 3, though, we still have another option: exchangability within the levels of the confounders. Put another way, we need exchangeability within levels of a valid adjustment set. In this case, there is only one such set: customer_type.
satisfaction_strat <- satisfaction1 |>
group_by(customer_type, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
)
satisfaction_strat# A tibble: 4 × 3
customer_type update_frequency avg_satisfaction
<fct> <fct> <dbl>
1 free weekly -0.458
2 free daily -0.433
3 premium weekly 0.452
4 premium daily 0.463Let’s do a little wrangling to estimate the effect of update frequency on satisfaction within customer type levels. Now, we’re much closer to the right answer: within levels of customer type, there is no difference in satisfaction by update frequency.
satisfaction_strat_est <- satisfaction_strat |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(estimate = daily - weekly)
satisfaction_strat_est# A tibble: 2 × 1
estimate
<dbl>
1 0.0252
2 0.0110We can now take the overall average, giving us an effect close to 0.
satisfaction_strat_est |>
# note: we would need to weight this if the confounder
# groups were not equally sized
summarise(estimate = mean(estimate))# A tibble: 1 × 1
estimate
<dbl>
1 0.0181Now, let’s consider this approach with two binary confounders. Let’s assume that there was a second confounder: whether or not it was business hours. Weekly updates have a higher chance of occurring within business hours, while daily updates have a higher chance of occurring after business hours. Some customers overlap well with the company’s business hours, while some don’t; those who don’t have lower satisfaction due to the unavailability of customer service during their work hours.
Code
dag2 <- dagify(
satisfaction ~ customer_service + customer_type,
customer_service ~ business_hours,
updates ~ customer_type + business_hours,
coords = time_ordered_coords(),
labels = c(
customer_type = "customer\ntype",
business_hours = "business\nhours",
updates = "frequency\nof updates",
customer_service = "customer\nservice",
satisfaction = "customer\nsatisfaction"
)
)
ggdag(dag2, use_text = FALSE) +
geom_dag_text(
aes(label = label),
nudge_y = c(-.35, -.35, .35, .35, .35),
color = "black"
) +
theme_dag()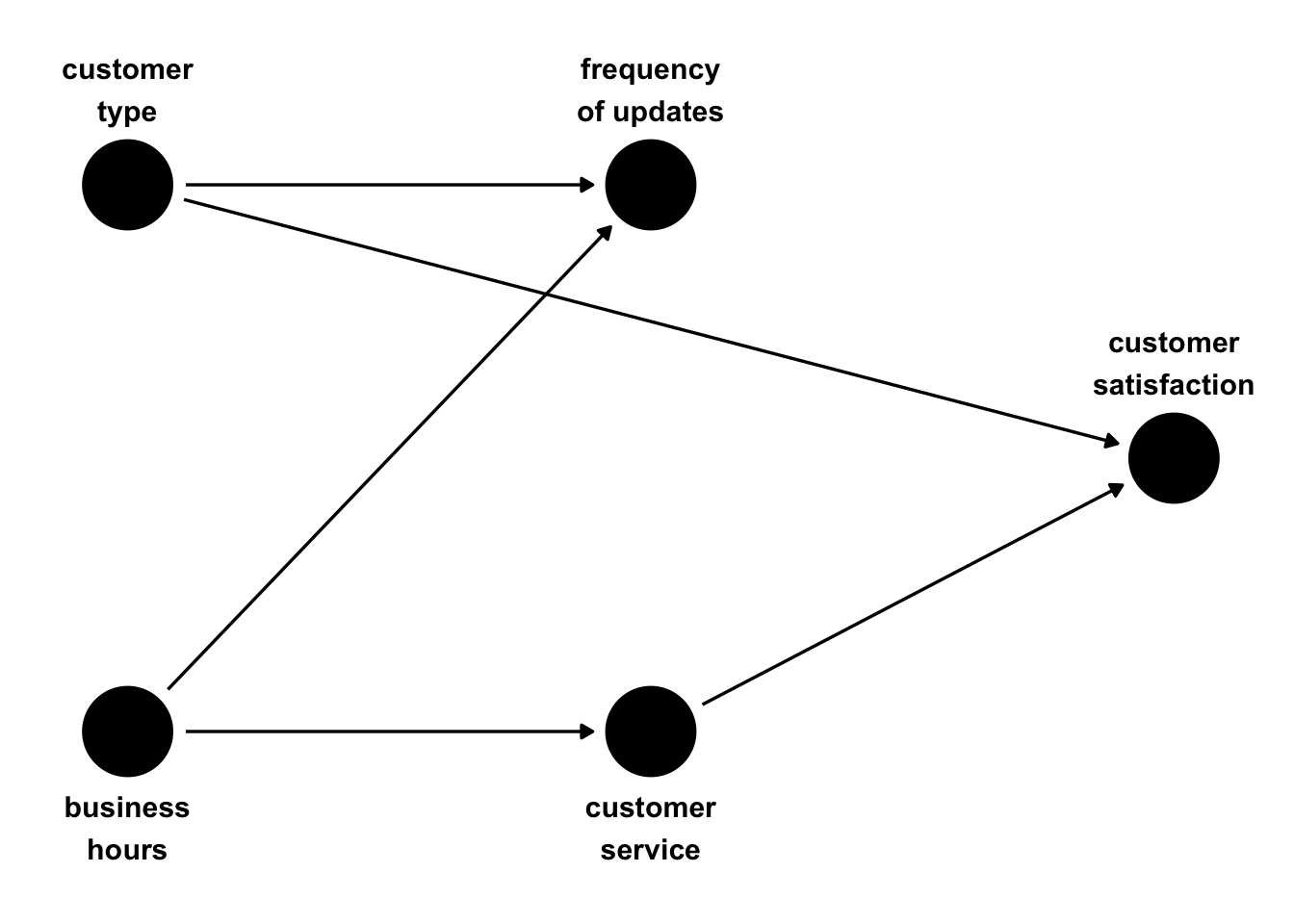
Let’s simulate this data:
satisfaction2 <- tibble(
# Free (0) or Premium (1)
customer_type = rbinom(n, 1, 0.5),
# Business hours (Yes: 1, No: 0)
business_hours = rbinom(n, 1, 0.5),
p_exposure = case_when(
customer_type == 1 & business_hours == 1 ~ 0.75,
customer_type == 0 & business_hours == 1 ~ 0.9,
customer_type == 1 & business_hours == 0 ~ 0.2,
customer_type == 0 & business_hours == 0 ~ 0.1
),
# Weekly (0) vs Daily (1)
update_frequency = rbinom(n, 1, p_exposure),
# More likely during business hours
customer_service_prob = business_hours * 0.9 +
(1 - business_hours) * 0.2,
customer_service = rbinom(n, 1, prob = customer_service_prob),
satisfaction = 70 + 10 * customer_type +
15 * customer_service + rnorm(n),
) |>
mutate(
satisfaction = as.numeric(scale(satisfaction)),
customer_type = factor(
customer_type,
labels = c("free", "premium")
),
business_hours = factor(
business_hours,
labels = c("no", "yes")
),
update_frequency = factor(
update_frequency,
labels = c("weekly", "daily")
),
customer_service = factor(
customer_service,
labels = c("no", "yes")
)
)We now need exchangeability within levels two confounders. In this case, we have two minimal adjustment sets: customer_type + business_hours and customer_type + customer_service. Let’s look at each.
Within combinations of customer_type and business_hours, the update frequency groups are very close.
satisfaction2_strat <- satisfaction2 |>
group_by(customer_type, business_hours, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
)
satisfaction2_strat |>
select(avg_satisfaction, everything())# A tibble: 8 × 4
avg_satisfaction customer_type business_hours
<dbl> <fct> <fct>
1 -1.14 free no
2 -1.16 free no
3 -0.0216 free yes
4 0.0180 free yes
5 -0.0493 premium no
6 -0.0673 premium no
7 1.13 premium yes
8 1.12 premium yes
# ℹ 1 more variable: update_frequency <fct>With a little more wrangling than before, we can calculate the overall estimate.
satisfaction2_strat |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(estimate = mean(daily - weekly))# A tibble: 1 × 1
estimate
<dbl>
1 -0.00415We can also achieve conditional exchangeability within levels of customer_type and customer_service. The answers are slightly different because of chance differences between the variables we’ve chosen to account for, but we get close to null for both approaches.
satisfaction2 |>
group_by(customer_type, customer_service, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
) |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(estimate = mean(daily - weekly))# A tibble: 1 × 1
estimate
<dbl>
1 -0.00196As long as we have enough data, this approach extends nicely with many confounders, including categorical confounders. What about a continuous confounder?
Instead of the binary confounders, let’s say we have one continuous confounder: the number of users within the organization, as in Figure 6.3.
Code
coords3 <- list(
x = c(num_users = 1, updates = 2, satisfaction = 3),
y = c(num_users = 0, updates = 0, satisfaction = 0)
)
dag3 <- dagify(
satisfaction ~ num_users,
updates ~ num_users,
coords = coords3,
labels = c(
num_users = "number of\nusers",
updates = "frequency\nof updates",
satisfaction = "customer\nsatisfaction"
)
)
ggdag(dag3, use_text = FALSE, use_edges = FALSE) +
geom_dag_text(aes(label = label), nudge_y = c(-.05, -.05, -.05), color = "black") +
geom_dag_edges_arc(curvature = c(0.07, 0)) +
theme_dag() +
ylim(c(.2, -.2))Organizations with more users get more updates and have slightly lower satisfaction scores.
satisfaction3 <- tibble(
# Number of users
num_users = runif(n, min = 1, max = 500),
# Larger customers more likely to have daily updates
update_frequency = rbinom(n, 1, plogis(num_users / 100)),
# with more users come less satisfaction
satisfaction = 70 + -0.2 * num_users + rnorm(n)
) |>
mutate(
satisfaction = as.numeric(scale(satisfaction)),
update_frequency = factor(
update_frequency,
labels = c("weekly", "daily")
)
)If we still want to use group_by and summarize(), we could bin the continuous confounder, for example, using its quintiles, and estimate the causal effect within each bin:
satisfaction3_strat <- satisfaction3 |>
mutate(num_users_q = ntile(num_users, 5)) |>
group_by(num_users_q, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
)
satisfaction3_strat# A tibble: 10 × 3
num_users_q update_frequency avg_satisfaction
<int> <fct> <dbl>
1 1 weekly 1.41
2 1 daily 1.37
3 2 weekly 0.725
4 2 daily 0.682
5 3 weekly 0.0459
6 3 daily -0.00825
7 4 weekly -0.631
8 4 daily -0.689
9 5 weekly -1.36
10 5 daily -1.39 We get around the correct answer within binned levels of users. Let’s get the overall mean:
satisfaction3_strat |>
ungroup() |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(estimate = mean(daily - weekly))# A tibble: 1 × 1
estimate
<dbl>
1 -0.0455As opposed to binary and categorical confounders, grouping by bins for continuous confounders does not completely account for the variable; the coarser the bins, the more residual confounding there will be, and the finer the bins, the closer we’ll get to the continuous version (but the fewer values we’ll have per bin, see Tip 6.1).
Let’s see what happens if we increase the number of bins. In the figure below, we’ve changed the number of bins from 5 in the example in the text to range from 3 to 20. Notice as we increase the number of bins the bias decreases.
Code
update_bins <- function(bins) {
satisfaction3 |>
mutate(num_users_q = ntile(num_users, bins)) |>
group_by(num_users_q, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
) |>
ungroup() |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(
bins = bins,
estimate = mean(daily - weekly)
)
}
map(3:20, update_bins) |>
bind_rows() |>
ggplot(aes(x = bins, y = abs(estimate))) +
geom_point() +
geom_line() +
labs(y = "Bias", x = "Number of bins")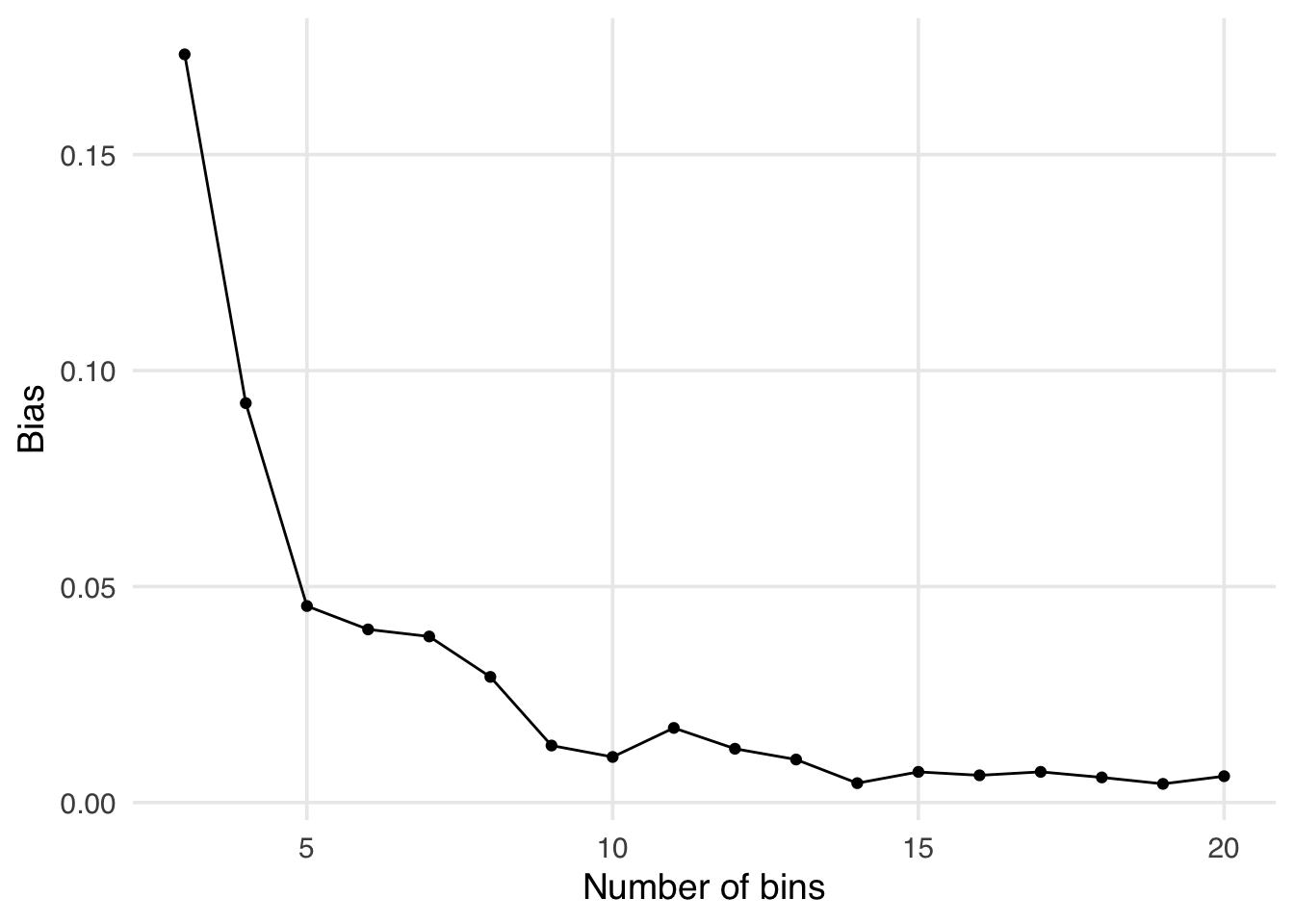
For example, looking at the output below we see that the estimate is much closer to the truth (0) when we have 20 bins compared to 5.
satisfaction3 |>
mutate(num_users_q = ntile(num_users, 20)) |>
group_by(num_users_q, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
) |>
ungroup() |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(estimate = mean(daily - weekly))# A tibble: 1 × 1
estimate
<dbl>
1 -0.00609As with many good things, however, there is a limit to the utility of increasing the number of bins. For example, let’s see what happens if we try to have 30 bins.
satisfaction3 |>
mutate(num_users_q = ntile(num_users, 30)) |>
group_by(num_users_q, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
) |>
ungroup() |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(estimate = mean(daily - weekly))# A tibble: 1 × 1
estimate
<dbl>
1 NAThe estimate is NA because some of our bins didn’t have anyone in one of the exposure groups, making their difference inestimable. Now, this analysis violates our positivity assumption. This is a stochastic violation; it has to do with our sample size, 10,000, and the number of bins, 30. By chance, we ended up with at least one of the 30 bins without anyone in one of the exposure groups, making our causal effect inestimable. This non-parametric method, while flexible, has limitations due to the sample size. Parametric models are useful because they allow us to extrapolate under certain assumptions, which makes them more efficient (assuming our assumptions are true, let’s learn more in Section 6.2).
The approach we’ve been using with group_by() and summarize() is often called stratification. You can also think of it as a type of non-parametric approach. We aren’t using any parameterization from a statistical model to restrict the form of the variables the way we might with, say, a linear regression. (This is only partially true for continuous confounders because it’s not practical to stratify by all values of the continuous variable).
Stratification can be powerful for simple problems or when you have lots of data because you can sometimes avoid model misspecification problems. However, with many confounders (especially continuous ones), we quickly encounter the curse of dimensionality, making it impractical because we have too few observations by combinations of confounder levels.
6.2 Parametric outcome models
You can think of stratification as calculating conditional means. A more general extension of conditional means is multivariable linear regression. When we fit lm() with the variables in the form outcome ~ exposure + confounder1 + confounder2 + ..., we are fitting what we call an outcome model, so called because we fit the exposure and confounders with the outcome as the dependent variable. This is also sometimes called direct adjustment or regression adjustment because we adjust for the confounders directly in the regression model. Let’s use lm() to calculate the effect in our example with two binary confounders:
library(broom)
lm(
satisfaction ~ update_frequency + customer_type + business_hours,
data = satisfaction2
) |>
tidy(conf.int = TRUE) |>
filter(term == "update_frequencydaily") |>
select(estimate, starts_with("conf"))# A tibble: 1 × 3
estimate conf.low conf.high
<dbl> <dbl> <dbl>
1 -0.00906 -0.0411 0.0230It also works well for continuous confounders, as we no longer need to bin it to get the correct answer:
lm(
satisfaction ~ update_frequency + num_users,
data = satisfaction3
) |>
tidy(conf.int = TRUE) |>
filter(term == "update_frequencydaily") |>
select(estimate, starts_with("conf"))# A tibble: 1 × 3
estimate conf.low conf.high
<dbl> <dbl> <dbl>
1 0.00153 -0.000595 0.00366This generalization doesn’t come for free, though: we’ve now introduced a parametric statistical model to make estimates across the sparse regions of our data. The estimate we get for satisfaction ~ update_frequency + num_users gives us exactly the right answer because the statistical model underlying lm() perfectly matches our simulation. For example, the relationship between satisfaction and num_users is linear, so when we fit this model, we don’t suffer from the problem of dimensionality (although linear regression has its own limits in terms of the number of rows and columns). In other words, we’re now dependent on the correct functional form, the mathematical representation of the relationship between variables in a model (See Tip 6.2 for more details). We need the correct functional form for both the exposure and the confounders. Modeling this well requires an understanding of the nature of the relationship between these variables and the outcome.
In the text we simulated the relationship between the outcome and the confounders to be linear, that is, it exactly met the assumptions underlying lm(), so we got the right answer when we fit our parameteric model. What would happen if our simulation did not match the assumptions underlying lm()? Let’s take a look.
set.seed(11)
satisfaction4 <- tibble(
# Number of users
num_users = runif(n, 1, 500),
# Larger customers more likely to have daily updates
update_frequency = rbinom(n, 1, plogis(num_users / 100)),
# non-linear relationship between satisfaction and number of users
satisfaction = 70 - 0.001 * (num_users-300)^2 - 0.001 * (num_users - 300)^3
) |>
mutate(
satisfaction = as.numeric(scale(satisfaction)),
update_frequency = factor(
update_frequency,
labels = c("weekly", "daily")
)
)
ggplot(satisfaction4, aes(x = num_users, y = satisfaction)) +
geom_line()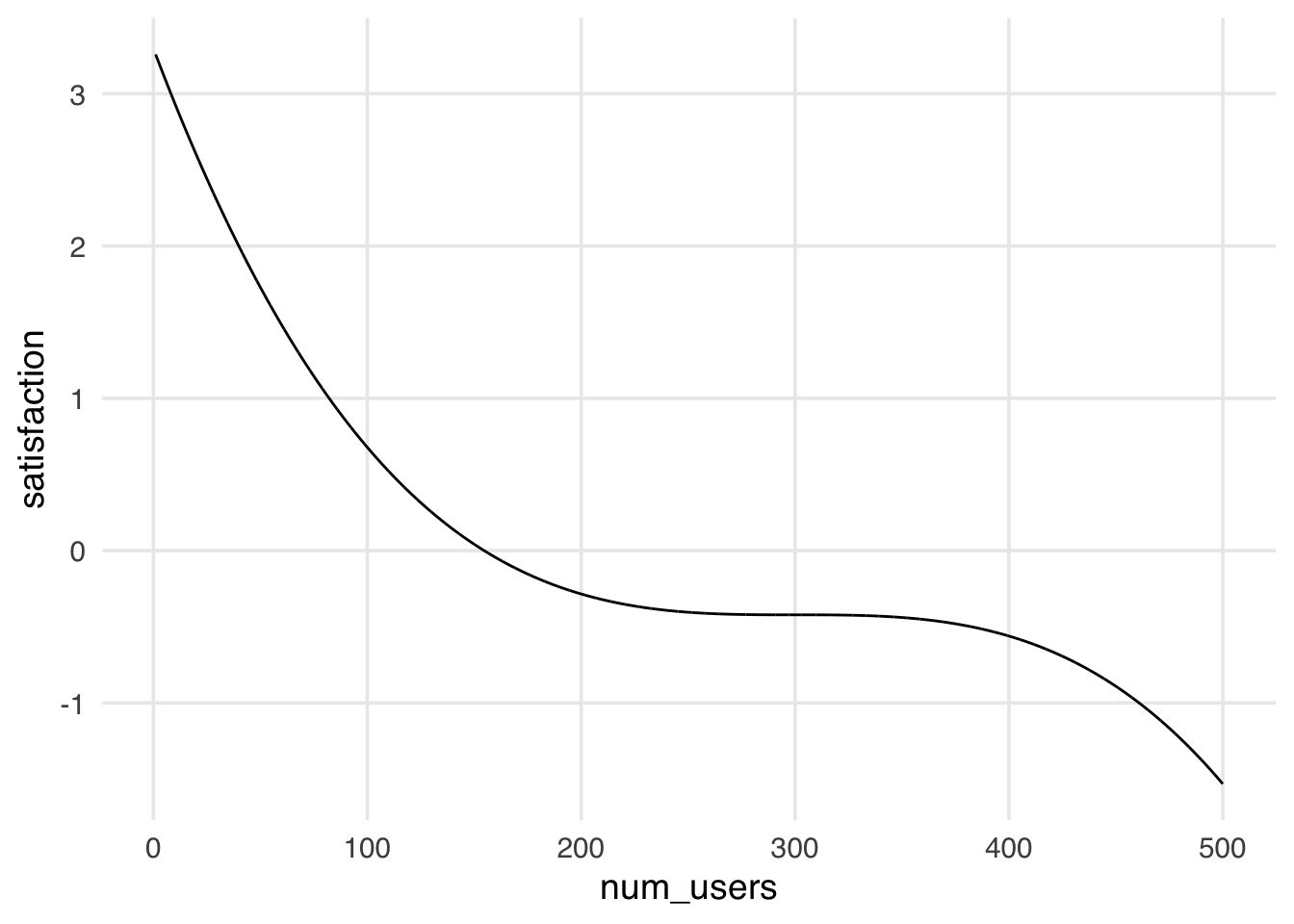
In the figure above we see that now there is a non-linear relationship between our confounder, number of users, and our outcome, satisfaction. Let’s see what happens if we fit an (incorrect) parameteric model to these data.
lm(
satisfaction ~ update_frequency + num_users,
data = satisfaction4
) |>
tidy(conf.int = TRUE) |>
filter(term == "update_frequencydaily") |>
select(estimate, starts_with("conf"))# A tibble: 1 × 3
estimate conf.low conf.high
<dbl> <dbl> <dbl>
1 -0.189 -0.219 -0.159Our estimates are far from the truth (which should be zero); the truth is not even contained in the confidence interval. What went wrong? Our parametric model assumed that the functional form of the relationship between the number of users and satisfaction was linear, but we generated it non-linearly. There is a solution that still allows for the use of a parametric model; if we knew the true functional form, we could use that. Let’s see how that looks.
lm(
satisfaction ~ update_frequency + poly(num_users, 3),
data = satisfaction4
) |>
tidy(conf.int = TRUE) |>
filter(term == "update_frequencydaily") |>
select(estimate, starts_with("conf"))# A tibble: 1 × 3
estimate conf.low conf.high
<dbl> <dbl> <dbl>
1 1.86e-15 1.58e-15 2.13e-15Beautiful! Now, this model was fit exactly as the data were generated, and again, we ended up with the exact right answer. In the real world, we often do not know the data-generating mechanism, but we can still fit flexible parametric models. A great way to do this is through natural cubic splines.
lm(
satisfaction ~ update_frequency + splines::ns(num_users, 3),
data = satisfaction4
) |>
tidy(conf.int = TRUE) |>
filter(term == "update_frequencydaily") |>
select(estimate, starts_with("conf"))# A tibble: 1 × 3
estimate conf.low conf.high
<dbl> <dbl> <dbl>
1 0.00216 -0.00258 0.00690We can also use our original non-parametric method; if we stratify this into 20 bins, we also get a less biased estimate (i.e., it is very close to the true value, 0).
satisfaction4_strat <- satisfaction4 |>
mutate(num_users_q = ntile(num_users, 20)) |>
group_by(num_users_q, update_frequency) |>
summarise(
avg_satisfaction = mean(satisfaction),
.groups = "drop"
)
satisfaction4_strat |>
ungroup() |>
pivot_wider(
names_from = update_frequency,
values_from = avg_satisfaction
) |>
summarise(estimate = mean(daily - weekly))# A tibble: 1 × 1
estimate
<dbl>
1 -0.00817We’ll also later explore ways to use data-adaptive methods like machine learning to reduce this assumption (Chapter 21).
Outcome regression can work very well when we meet the assumptions of the estimator we’re using for our model. OLS, for instance, can be very beneficial if we understand the relationships between the outcome and the variables in the regression, and we believe the assumptions of the model, particularly linearity. It’s very efficient, statistically (meaning we’ll get a small standard error). We’ll also get nominally correct confidence intervals without needing to bootstrap (Appendix A). Scientists and other people who analyze data are also usually familiar with linear regression, making it easier for many to understand what you did to calculate the causal effect. In fact, you could say that when there is a linear relationship between the outcome and exposure, and we meet the causal assumptions laid out in Section 3.2, correlation is causation.
So, why don’t we always use outcome models to calculate causal effects? First, we may be more confident in modeling the exposure instead of the outcome (as in inverse probability models, for instance). We’ll explore this idea more in Chapter 13 and Chapter 20. Relatedly, when we have a binary outcome, it may make sense to choose one over another based on the number of events. For example, using a propensity score method can be more statistically efficient if the outcome is rare but the exposure is not. Second, it can sometimes be challenging to get the estimate we are targeting with outcome models—an answer to a precise question—something we will probe more deeply in Chapter 10.
Relatedly, outcome models give us conditional effects. In other words, when describing the estimated coefficient, we often say something like “a one-unit change in the exposure results in a coefficient change in the outcome holding all other variables in the model constant”. In causal inference, we are often interested in marginal effects. Mathematically, this means that we want to average the effect of interest across the distribution of factors in a particular population for which we are trying to estimate a causal effect. In the case where the outcome is continuous, the effect is linear, and there are no interactions between the exposure effect and other factors about the population, the distinction between a conditional and a marginal effect is largely semantic. The estimates will be identical.
If there is an interaction in the model, that is, if the exposure has a different impact on the outcome depending on some other factor, we no longer have a single coefficient to interpret. We may want to estimate a marginal effect, taking into account the distribution of that factor in the population of interest. Why? We are ultimately trying to determine whether we should suggest exposure to the target population, so we want to know, on average, whether it will be beneficial.
Consider a variation of Figure 6.1 where update frequency does have a causal effect, but that effect varies by customer type. For premium customers, daily updates increase satisfaction by 5 points. For free customers, daily updates decrease satisfaction by 5 points. The effect of changing the update frequency is heterogeneous, depending on customer type. Whether increasing the update frequency to daily for everyone is beneficial depends on the distribution of premium vs. free customers.
-
If 50% of the customers are premium and 50% are free, the average effect of switching to daily updates would be:
-
If 100% of the customers are premium, the average effect would be:
-
If 100% of the customers are free, the average effect would be:
Marginalization tells us the average effect for the distribution of covariates in the data. Of course, we might want to estimate the causal effect by customer type; we’ll discuss interaction effects in depth in Chapter 14.
Conditional effects are even more complex with logistic and Cox regression models; as we’ll see in Section 10.4.2, conditional coefficients for models like these estimate answers to entirely different questions depending on the variables in the model.
There are also times when we can’t use an outcome model. The first is when we don’t think we can meet the assumptions for unconfoundedness methods. In that case, we can’t use inverse probability weighting and friends, either. However, we may be able to use another method, such as instrumental variable analysis, regression discontinuity, or difference-in-differences (Chapter 22 and Chapter 23; we’ll also summarize these methods below). The second is when we have time-varying exposures and confounding. Linear regression cannot estimate these types of effects without bias, so we’ll need methods like inverse probability weighting or g-computation to calculate it correctly. Throughout most of the book, we’ll analyze simple pre-post data: we have baseline data, an exposure that happens at a single time point, and an outcome that occurs after exposure. In Chapter 18 and other chapters, we’ll cover more complex questions and data.
6.3 Overview of estimators for causal inference
As we’ve seen, it’s possible to do causal inference with simple methods like stratification and multivariable linear regression. For the rest of the book, however, we will focus on other causal methods, which allow us more flexibility in answering the questions we want to ask. Here’s a brief summary of some of the unconfoundedness methods we’ll cover and what they do.
-
Unconfoundedness methods
- Inverse probability weighting (propensity score weighting): Using a propensity score (predicted probability of treatment), we reweight units to create a pseudo-population where exchangeability holds. Extends to time-varying treatments.
- Matching (propensity score matching and other methods): Find treated and untreated units with similar propensity scores (or other measures of similarity) to match, creating a subpopulation where exchangeability holds.
- G-computation (also called standardization or marginal effects): Fit an outcome model but marginalize to get a marginal effect estimate. Extends to time-varying treatments.
- Doubly robust methods: Fit models for both the outcome and treatment. Using doubly robust methods, only one of these models needs to be correct for the estimate to be correct. Doubly robust methods also allow us to use machine learning algorithms. We’ll discuss targeted learning (TMLE) and augmented propensity scores.
While the book focuses primarily on unconfoundedness methods, we later cover methods that make other assumptions (Chapter 22 and Chapter 23). Here’s a brief summary of when we might want to explore these methods instead of trying to achieve exchangeability:
- Instrumental variables: There’s a variable (the instrument) that affects the treatment but does not directly affect the outcome except through the treatment. Because it’s effectively random, we can use it to estimate a type of causal effect.
- Regression discontinuity: There’s a cutoff or threshold that determines who gets the treatment, and individuals just above or below the threshold are comparable. Regression discontinuity is closely related to instruments.
- Difference-in-differences: The treated and untreated groups would have followed the same trend over time in the absence of the treatment (they have parallel trends). If the two groups would have been identical sans treatment, we can use the untreated as a counterfactual for the treated.
- Synthetic controls: A weighted combination of untreated units can closely approximate the treated unit’s outcome without the treatment. Synthetic controls are closely related to difference-in-differences.
6.3.1 Causal methods in randomized trials
Randomized trials alleviate many of the assumptions we need to make for causal inference. When randomization has succeeded, we don’t need to control for any confounders because they don’t exist. However, causal methods can still be useful for randomized exposures.
Let’s consider a variation of Figure 6.2 in which the frequency of updates is randomized to each customer; customer type and business hours are still causes of customer satisfaction. In other words, they cause the outcome but not the exposure. We can use an unadjusted regression model or simple differences in means to get a valid effect. As we discussed in Chapter 4, however, including causes of the outcome that are not causes of the exposure can improve the statistical precision of an estimate. Let’s look at three approaches: an unadjusted OLS outcome model, an adjusted OLS outcome model (direct adjustment), and an inverse probability-weighted model. In Figure 6.4, all three methods give us an unbiased effect. The effect of the propensity score is marginal, while the effect of the outcome model is conditional. Because of the way we’ve simulated the data, the two types of effects are identical. The unadjusted method, however, has a wider confidence interval and, relatedly, a larger standard error. The direct adjustment method and inverse probability weighting have smaller standard errors and, thus, narrower confidence intervals. It has been shown mathematically that using propensity scores like this to adjust for baseline factors in a randomized trial will always improve precision compared to the unadjusted estimate and is equivalent to the precision gained from directly adjusting (Williamson, Forbes, and White 2014).
Code
satisfaction_randomized <- tibble(
# Free (0) or Premium (1)
customer_type = rbinom(n, 1, 0.5),
# Business hours (Yes: 1, No: 0)
business_hours = rbinom(n, 1, 0.5),
# Weekly (0) vs Daily (1), now random
update_frequency = rbinom(n, 1, 0.5),
# More likely during business hours
customer_service_prob = business_hours *
0.9 + (1 - business_hours) * 0.2,
customer_service = rbinom(n, 1, prob = customer_service_prob),
satisfaction = 70 + 10 * customer_type +
15 * customer_service + rnorm(n),
) |>
mutate(
satisfaction = as.numeric(scale(satisfaction)),
customer_type = factor(
customer_type,
labels = c("free", "premium")
),
business_hours = factor(
business_hours,
labels = c("no", "yes")
),
update_frequency = factor(
update_frequency,
labels = c("weekly", "daily")
),
customer_service = factor(
customer_service,
labels = c("no", "yes")
)
)
plot_estimates <- function(d) {
unadj_model <- lm(satisfaction ~ update_frequency, data = d) |>
tidy(conf.int = TRUE) |>
mutate(term = if_else(
term == "update_frequencydaily",
"update_frequency",
term
)) |>
filter(term == "update_frequency") |>
mutate(model = "unadjusted")
adj_model <- lm(
satisfaction ~ update_frequency + business_hours +
customer_type,
data = d
) |>
tidy(conf.int = TRUE) |>
mutate(term = if_else(
term == "update_frequencydaily",
"update_frequency",
term
)) |>
filter(term == "update_frequency") |>
mutate(model = "direct\nadjustment")
df <- d |>
mutate(across(where(is.factor), as.integer)) |>
mutate(update_frequency = update_frequency - 1) |>
as.data.frame()
x <- PSW::psw(
df,
"update_frequency ~ business_hours + customer_type",
weight = "ATE",
wt = TRUE,
out.var = "satisfaction"
)
psw_model <- tibble(
term = "update_frequency",
estimate = x$est.wt,
std.error = x$std.wt,
conf.low = x$est.wt - 1.96 * x$std.wt,
conf.high = x$est.wt + 1.96 * x$std.wt,
statistic = NA,
p.value = NA,
model = "inverse\nprobability\nweighting"
)
models <- bind_rows(unadj_model, adj_model, psw_model) |>
mutate(model = factor(
model,
levels = c(
"unadjusted",
"direct\nadjustment",
"inverse\nprobability\nweighting"
)
))
models |>
select(model, estimate, std.error, starts_with("conf")) |>
pivot_longer(
c(estimate, std.error),
names_to = "statistic"
) |>
mutate(
conf.low = if_else(statistic == "std.error", NA, conf.low),
conf.high = if_else(statistic == "std.error", NA, conf.high),
statistic = case_match(
statistic,
"estimate" ~ "estimate (95% CI)",
"std.error" ~ "standard error"
)
) |>
ggplot(aes(value, fct_rev(model))) +
geom_point() +
geom_errorbarh(
aes(xmin = conf.low, xmax = conf.high),
height = 0
) +
facet_wrap(~statistic, scales = "free_x") +
theme(axis.title.y = element_blank())
}
plot_estimates(satisfaction_randomized)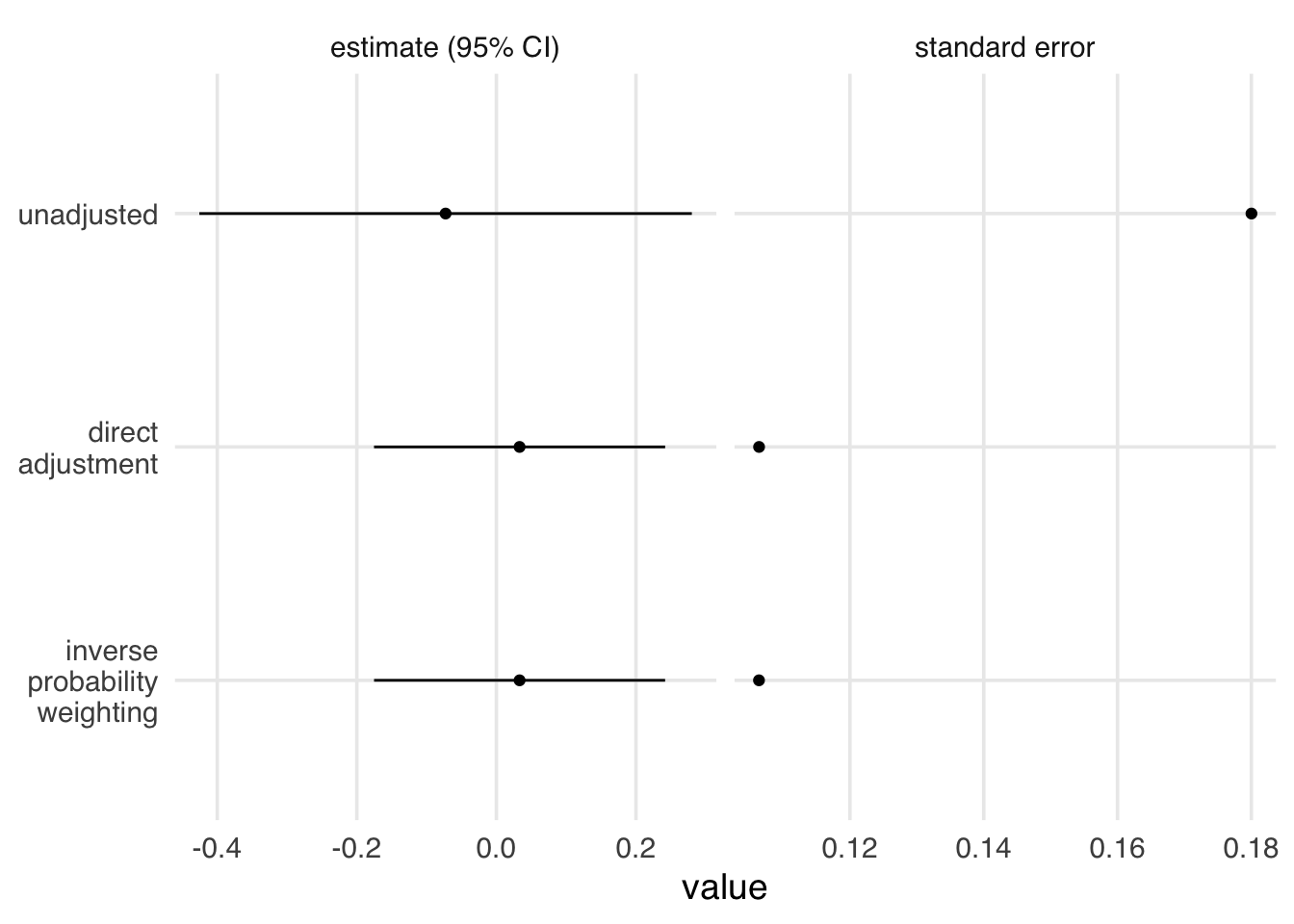
The two adjustment approaches, however, are not adjusting for confounders. Instead, they control the random variation in the data. For direct adjustment, we do this by accounting for variation in the outcome. For inverse probability weighting, we account for chance imbalances in the treatment groups across variables related to the outcome.
Causal methods can also help us address some of the violations of causal assumptions we saw in real-life randomized trials in Section 3.3. We’ll explore how these methods can help us address non-adherence and loss-to-follow-up, two common sources of bias in randomized trials, in Chapter 18 and Chapter 22.
6.4 Entering the design phase
Now, let’s turn our attention to an example with real data. We’re going to start with propensity score methods like matching and inverse probability weighting because they have a particular property: they allow us to model the relationship between exposure and confounders without peaking at the relationship between the exposure and outcome.
Let’s continue our journey to answering causal questions.