9 Evaluating your propensity score model

Work-in-progress 🚧

You are reading the work-in-progress first edition of Causal Inference in R. This chapter has its foundations written but is still undergoing changes.

Propensity scores are inherently balancing scores. The goal is to balance the exposure groups across confounders.

9.1 Calculating the standardized mean difference

One way to assess balance is the standardized mean difference. This measure helps you assess whether the average value for the confounder is balanced between exposure groups. For example, if you have some continuous confounder, $Z$ , and ${\bar{z}}_{e x p o s e d} = \frac{\sum Z_{i} (X_{i})}{\sum X_{i}}$ is the mean value of $Z$ among the exposed, ${\bar{z}}_{u n e x p o s e d} = \frac{\sum Z_{i} (1 - X_{i})}{\sum 1 - X_{i}}$ is the mean value of $Z$ among the unexposed, $s_{e x p o s e d}$ is the sample standard deviation of $Z$ among the exposed and $s_{u n e x p o s e d}$ is the sample standard deviation of $Z$ among the unexposed, then the standardized mean difference can be expressed as follows:

$d = \frac{{\bar{z}}_{e x p o s e d} - {\bar{z}}_{u n e x p o s u e d}}{\frac{\sqrt{s_{e x p o s e d}^{2} + s_{u n e x p o s e d}^{2}}}{2}}$ In the case of a binary $Z$ (a confounder with just two levels), $\bar{z}$ is replaced with the sample proportion in each group (e.g., ${\hat{p}}_{e x p o s e d}$ or ${\hat{p}}_{u n e x p o s e d}$ ) and $s^{2} = \hat{p} (1 - \hat{p})$ . In the case where $Z$ is categorical with more than two categories, $\bar{z}$ is the vector of proportions of each category level within a group and the denominator is the multinomial covariance matrix ( $S$ below), as the above can be written more generally as:

$d = \sqrt{({\bar{z}}_{e x p o s e d} - {\bar{z}}_{u n e x p o s e d})^{T} S^{- 1} ({\bar{z}}_{e x p o s e d} - {\bar{z}}_{u n e x p o s e d})}$

Often, we calculate the standardized mean difference for each confounder in the full, unadjusted, data set and then compare this to an adjusted standardized mean difference. If the propensity score is incorporated using matching, this adjusted standardized mean difference uses the exact equation as above, but restricts the sample considered to only those that were matched. If the propensity score is incorporated using weighting, this adjusted standardized mean difference weights each of the above components using the constructed propensity score weight.

In R, the halfmoon package has a function tidy_smd that will calculate this for a data set.

library(halfmoon)

smds <- tidy_smd(
  df,
  .vars = c(confounder_1, confounder_2, ...),
  .group = exposure,
  .wts = wts # weight is optional
)

Let’s look at an example using the same data as Section 8.2.

library(broom)
library(touringplans)
library(propensity)

seven_dwarfs_9 <- seven_dwarfs_train_2018 |> filter(wait_hour == 9)

seven_dwarfs_9_with_ps <-
  glm(
    park_extra_magic_morning ~ park_ticket_season + park_close + park_temperature_high,
    data = seven_dwarfs_9,
    family = binomial()
  ) |>
  augment(type.predict = "response", data = seven_dwarfs_9)
seven_dwarfs_9_with_wt <- seven_dwarfs_9_with_ps |>
  mutate(w_ate = wt_ate(.fitted, park_extra_magic_morning))

Now, using the tidy_smd function, we can examine the standardized mean difference before and after weighting.

library(halfmoon)
smds <-
  seven_dwarfs_9_with_wt |>
  mutate(park_close = as.numeric(park_close)) |>
  tidy_smd(
    .vars = c(park_ticket_season, park_close, park_temperature_high),
    .group = park_extra_magic_morning,
    .wts = w_ate
  )
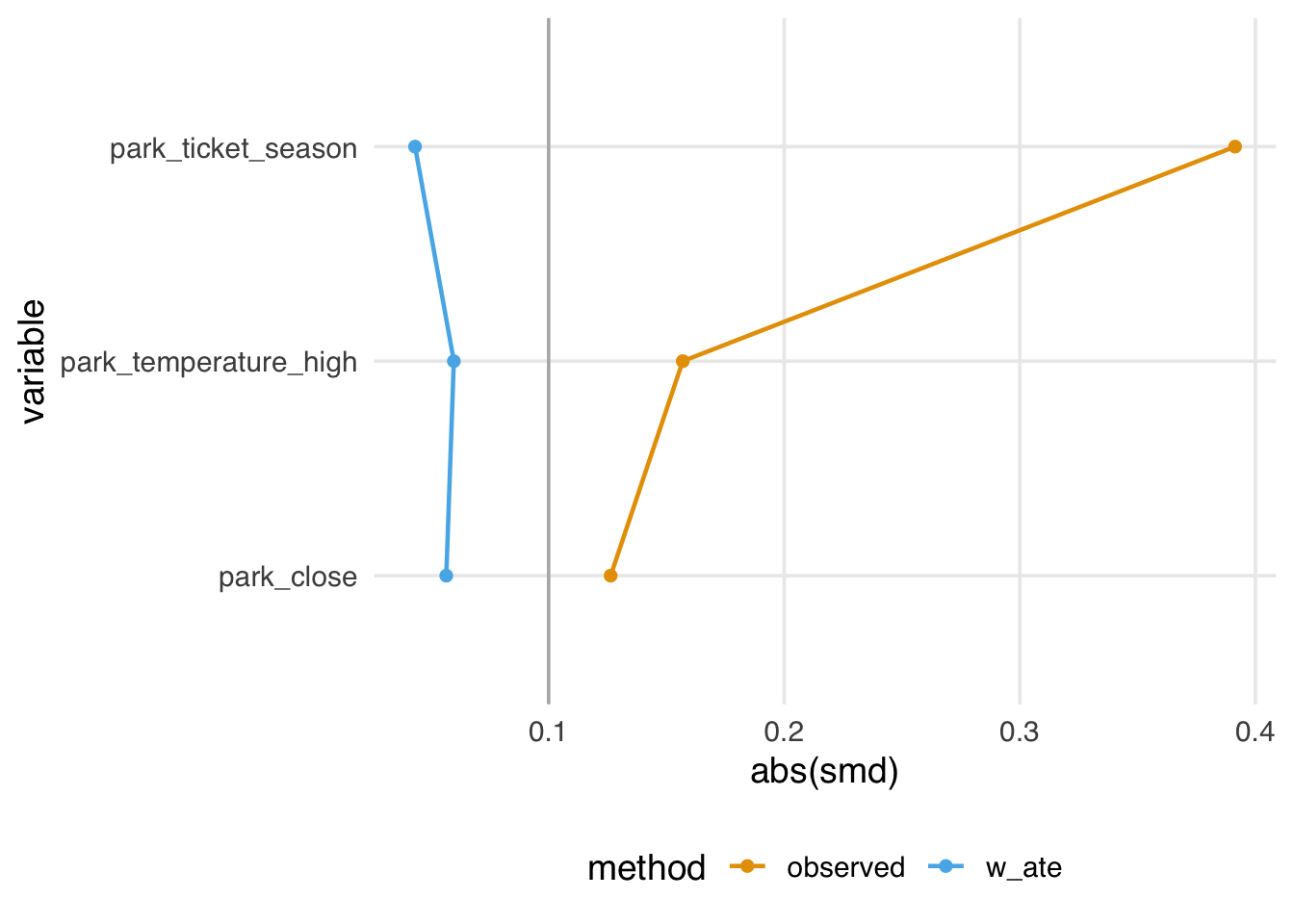
smds

# A tibble: 6 × 4
  variable        method park_extra_magic_mor…¹     smd
  <chr>           <chr>  <chr>                    <dbl>
1 park_ticket_se… obser… 1                       0.391 
2 park_close      obser… 1                       0.126 
3 park_temperatu… obser… 1                       0.157 
4 park_ticket_se… w_ate  1                       0.0433
5 park_close      w_ate  1                      -0.0566
6 park_temperatu… w_ate  1                       0.0598
# ℹ abbreviated name: ¹park_extra_magic_morning

For example, we see above that the observed standardized mean difference (prior to incorporating the propensity score) for ticket season is 0.39, however after incorporating the propensity score weight this is attenuated, now 0.04.

One downside of this metric is it only quantifying balance on the mean, which may not be sufficient for continuous confounders, as it is possible to be balanced on the mean but severely imbalanced in the tails. At the end of this chapter we will show you a few tools for examining balance across the full distribution of the confounder.

9.2 Visualizing balance

9.2.1 Love Plots

Let’s start by visualizing these standardized mean differences. To do so, we like to use a Love Plot (named for Thomas Love, as he was one of the first to popularize them). The halfmoon package has a function geom_love that simplifies this implementation.

ggplot(
  data = smds,
  aes(
    x = abs(smd),
    y = variable,
    group = method,
    color = method
  )
) +
  geom_love()

9.2.2 Boxplots and eCDF plots

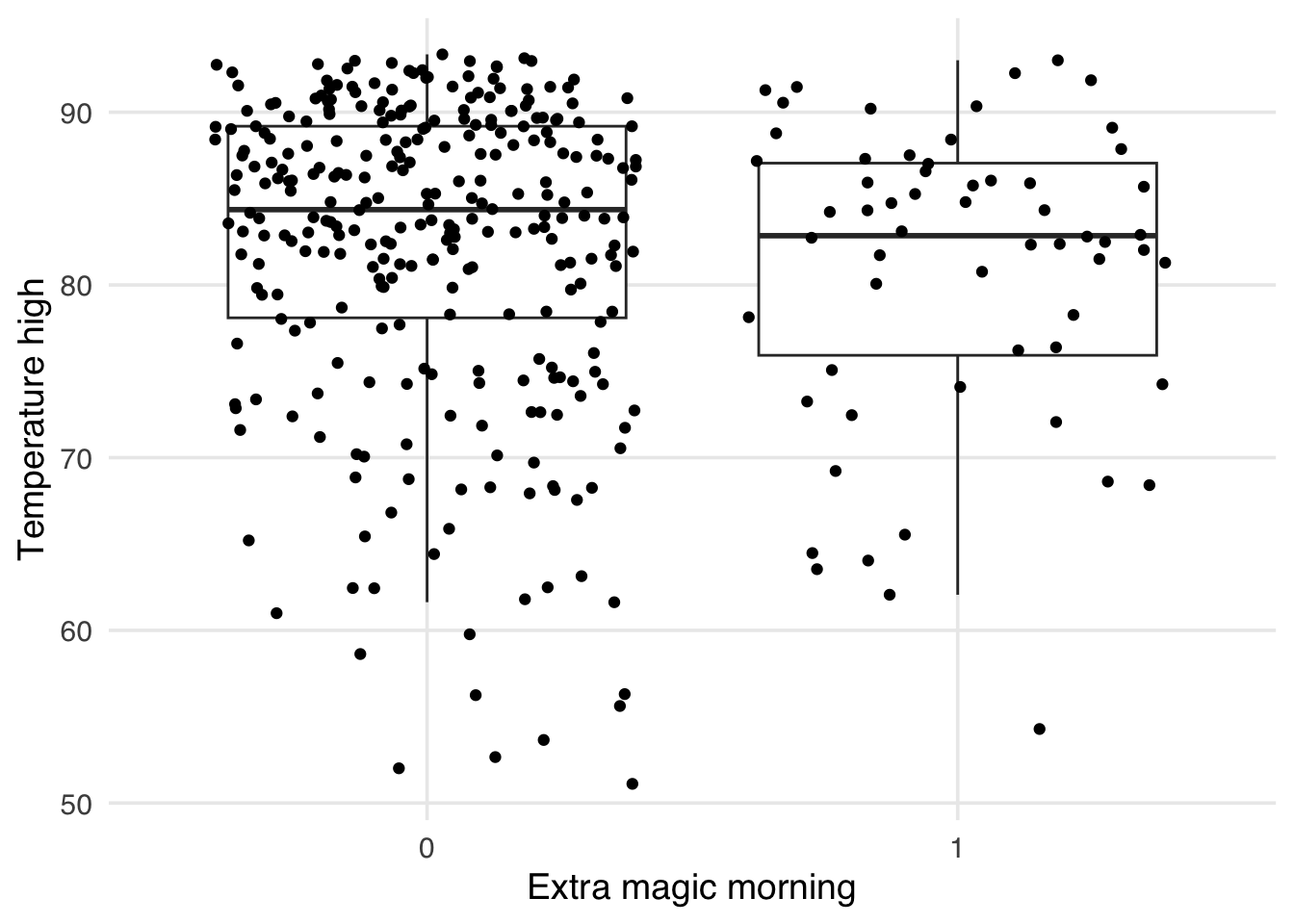
As mentioned above, one issue with the standardized mean differences is they only quantify balance on a single point for continuous confounders (the mean). It can be helpful to visualize the whole distribution to ensure that there is not residual imbalance in the tails. Let’s first use a boxplot. As an example, let’s use the park_temperature_high variable. When we make boxplots, we prefer to always jitter the points on top to make sure we aren’t masking and data anomolies – we use geom_jitter to accomplish this. First, we will make the unweighted boxplot.

ggplot(
  seven_dwarfs_9_with_wt,
  aes(
    x = factor(park_extra_magic_morning),
    y = park_temperature_high,
    group = park_extra_magic_morning
  )
) +
  geom_boxplot(outlier.color = NA) +
  geom_jitter() +
  labs(
    x = "Extra magic morning",
    y = "Temperature high"
  )

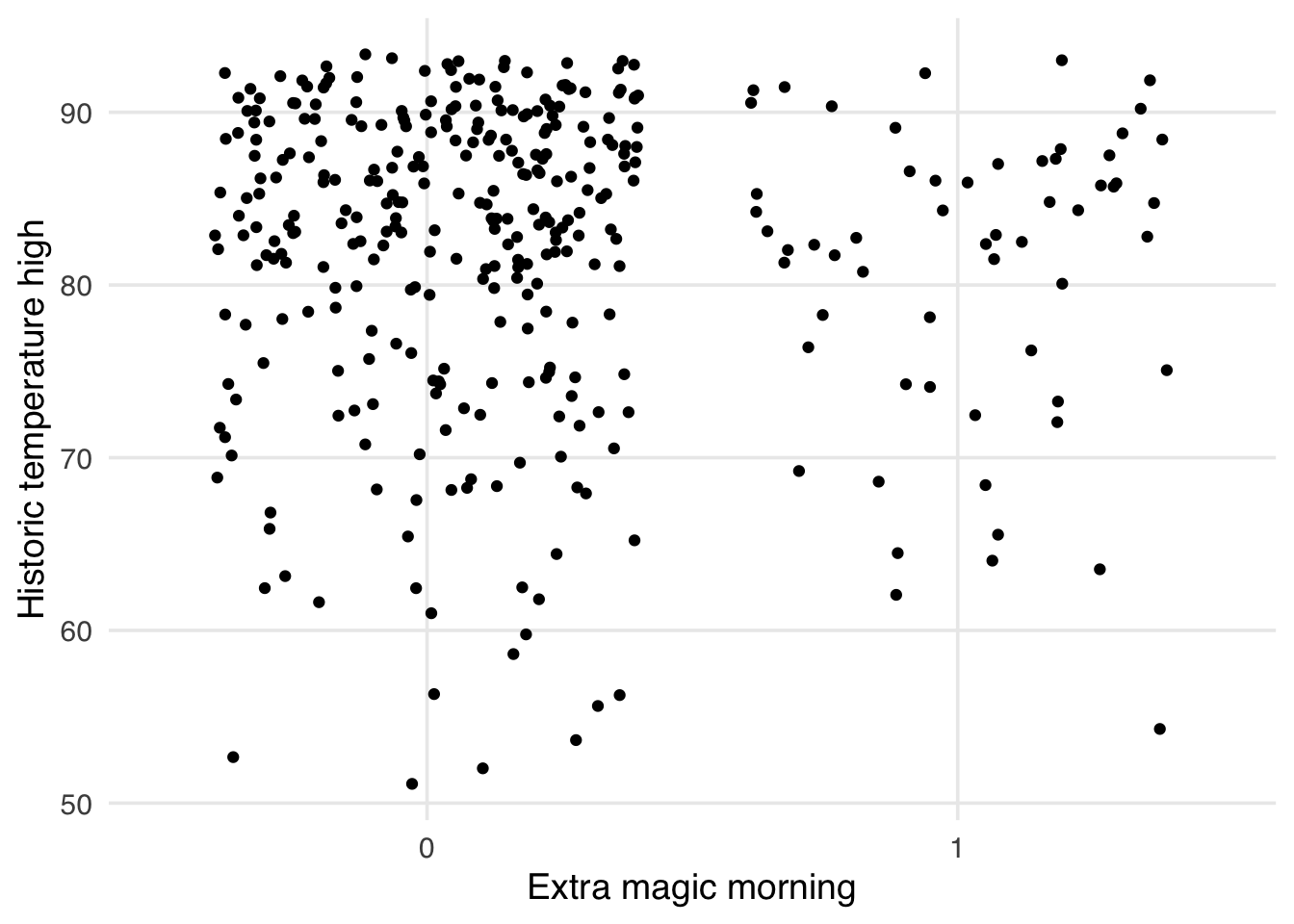
Figure 9.1: Unweighted boxplot showing the difference in historical high temperature between days that had extra magic hours and those that did not.

ggplot(
  seven_dwarfs_9_with_wt,
  aes(
    x = factor(park_extra_magic_morning),
    y = park_temperature_high,
    group = park_extra_magic_morning,
    weight = w_ate
  )
) +
  geom_boxplot(outlier.color = NA) +
  geom_jitter() +
  labs(
    x = "Extra magic morning",
    y = "Historic temperature high"
  )

Figure 9.2: Weighted boxplot showing the difference in historical high temperature between days that had extra magic hours and those that did not after incorporating the propensity score weight (ATE weight).

Similarly, we can also examine the empirical cumulative distribution function (eCDF) for the confounder stratified by each exposure group. The unweighted eCDF can be visualized using geom_ecdf

ggplot(
  seven_dwarfs_9_with_wt,
  aes(
    x = park_temperature_high,
    color = factor(park_extra_magic_morning)
  )
) +
  geom_ecdf() +
  scale_color_manual(
    "Extra Magic Morning",
    values = c("#5154B8", "#5DB854"),
    labels = c("Yes", "No")
  ) +
  labs(
    x = "Historic temperature high",
    y = "Proportion <= x"
  )

Figure 9.3: Unweighted eCDF examining the difference in distribution for historic high temperature among days that had extra magic morning hours (purple) compared to those that did not (green).

The halfmoon package allows for the additional weight argument to be passed to geom_ecdf to display a weighted eCDF plot.

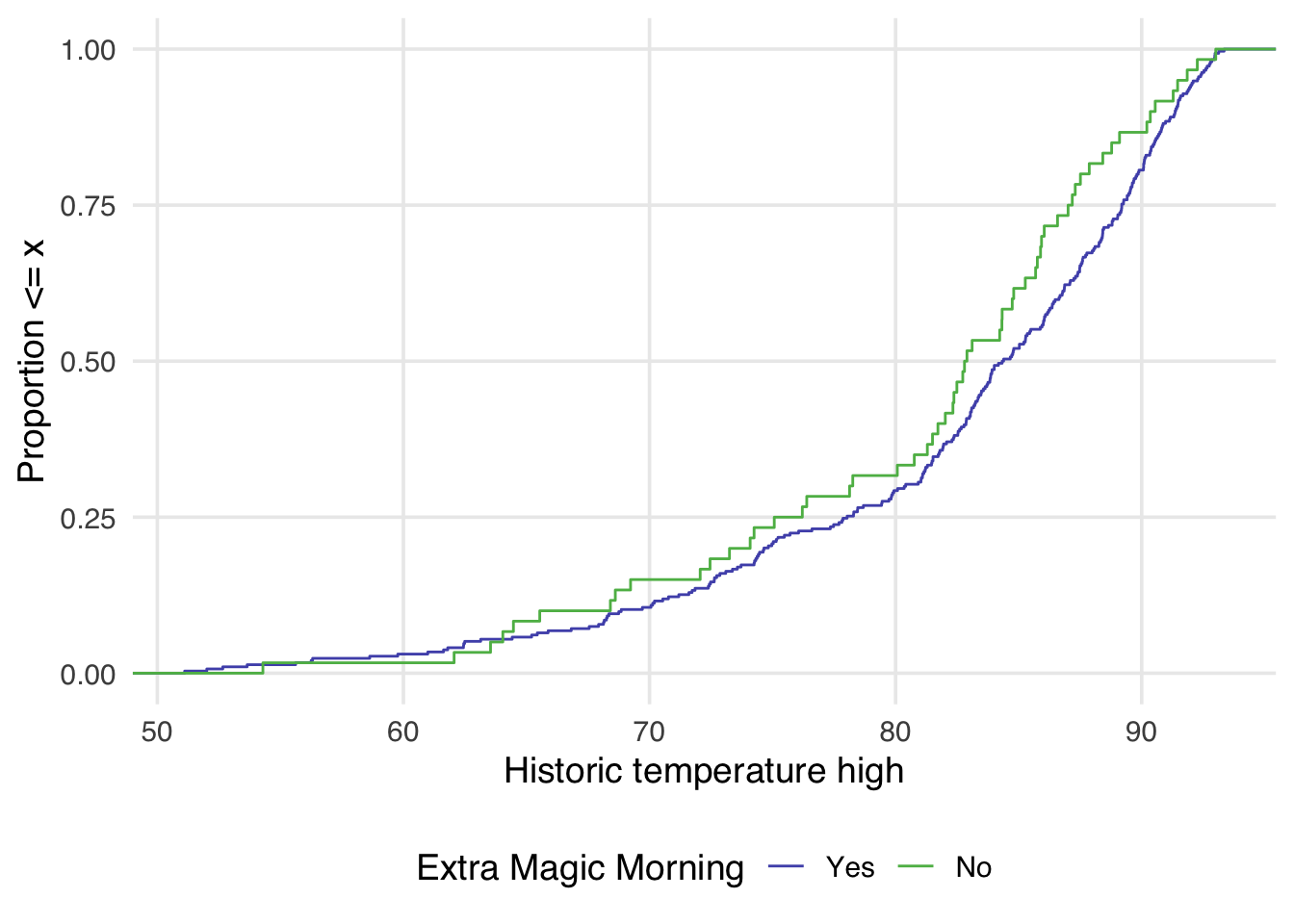
ggplot(
  seven_dwarfs_9_with_wt,
  aes(
    x = park_temperature_high,
    color = factor(park_extra_magic_morning)
  )
) +
  geom_ecdf(aes(weights = w_ate)) +
  scale_color_manual(
    "Extra Magic Morning",
    values = c("#5154B8", "#5DB854"),
    labels = c("Yes", "No")
  ) +
  labs(
    x = "Historic temperature high",
    y = "Proportion <= x"
  )

Figure 9.4: Weighted eCDF examining the difference in distribution for historic high temperature among days that had extra magic morning hours (purple) compared to those that did not (green) after incorporating the propensity score weight (ATE).

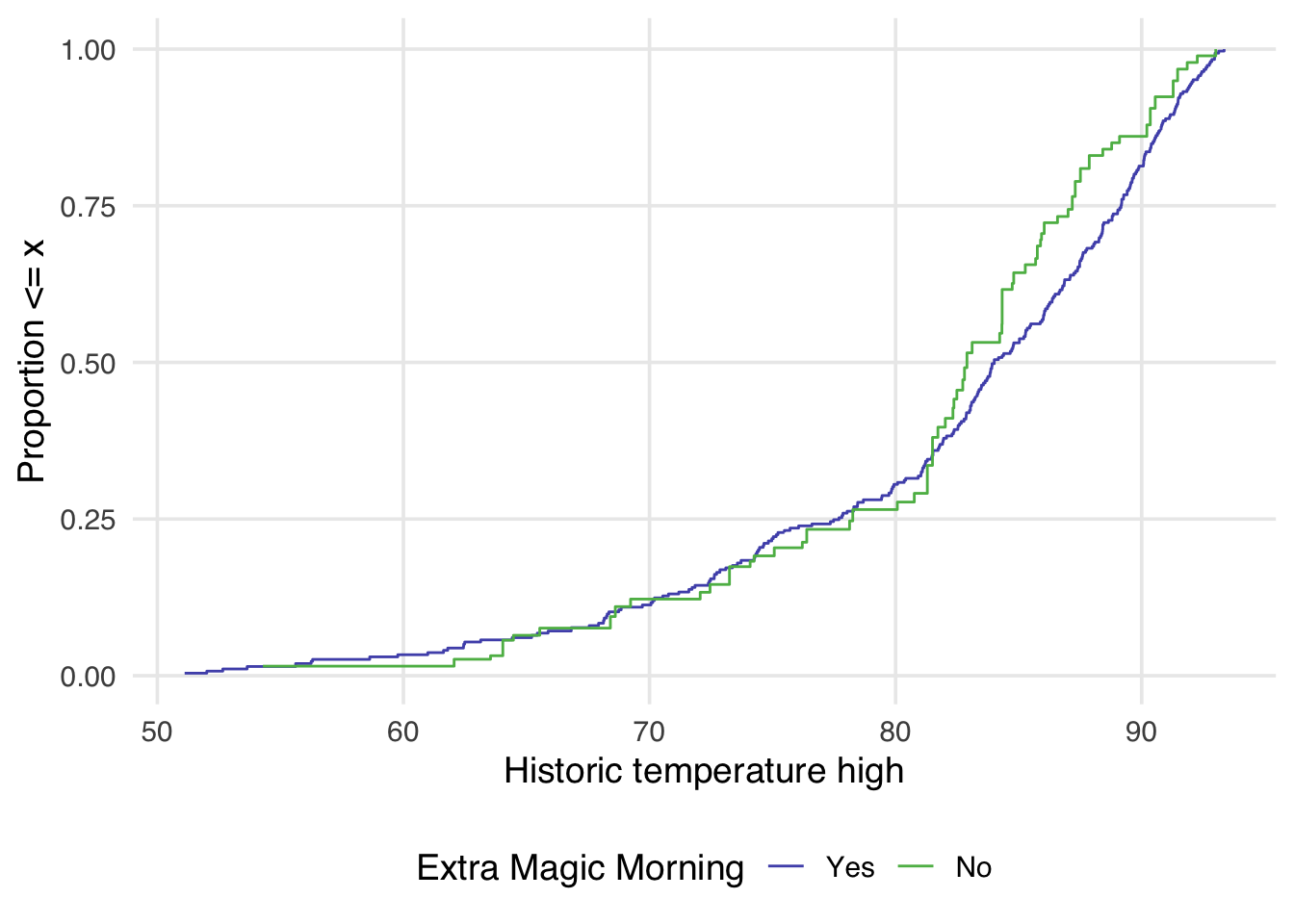
Examining Figure 9.4, we can notice a few things. First, compared to Figure 9.3 there is improvement in the overlap between the two distributions. In Figure 9.3, the green line is almost always noticeably above the purple, whereas in Figure 9.4 the two lines appear to mostly overlap until we reach slightly above 80 degrees. After 80 degrees, the lines appear to diverge in the weighted plot. This is why it can be useful to examine the full distribution rather than a single summary measure. If we had just used the standardized mean difference, for example, we would have likely said these two groups are balanced and moved on. Looking at Figure 9.4 suggests that perhaps there is a non-linear relationship between the probability of having an extra magic morning and the historic high temperature. Let’s try refitting our propensity score model using a natural spline. We can use the function splines::ns for this.

seven_dwarfs_9_with_ps <-
  glm(
    park_extra_magic_morning ~ park_ticket_season + park_close +
      splines::ns(park_temperature_high, df = 5), # refit model with a spline
    data = seven_dwarfs_9,
    family = binomial()
  ) |>
  augment(type.predict = "response", data = seven_dwarfs_9)
seven_dwarfs_9_with_wt <- seven_dwarfs_9_with_ps |>
  mutate(w_ate = wt_ate(.fitted, park_extra_magic_morning))

Now let’s see how that impacts the weighted eCDF plot

ggplot(
  seven_dwarfs_9_with_wt,
  aes(
    x = park_temperature_high,
    color = factor(park_extra_magic_morning)
  )
) +
  geom_ecdf(aes(weights = w_ate)) +
  scale_color_manual(
    "Extra Magic Morning",
    values = c("#5154B8", "#5DB854"),
    labels = c("Yes", "No")
  ) +
  labs(
    x = "Historic temperature high",
    y = "Proportion <= x"
  )

Figure 9.5: Weighted eCDF examining the difference in distribution for historic high temperature among days that had extra magic morning hours (purple) compared to those that did not (green) after incorporating the propensity score weight where historic high temperature was modeled flexibly with a spline.

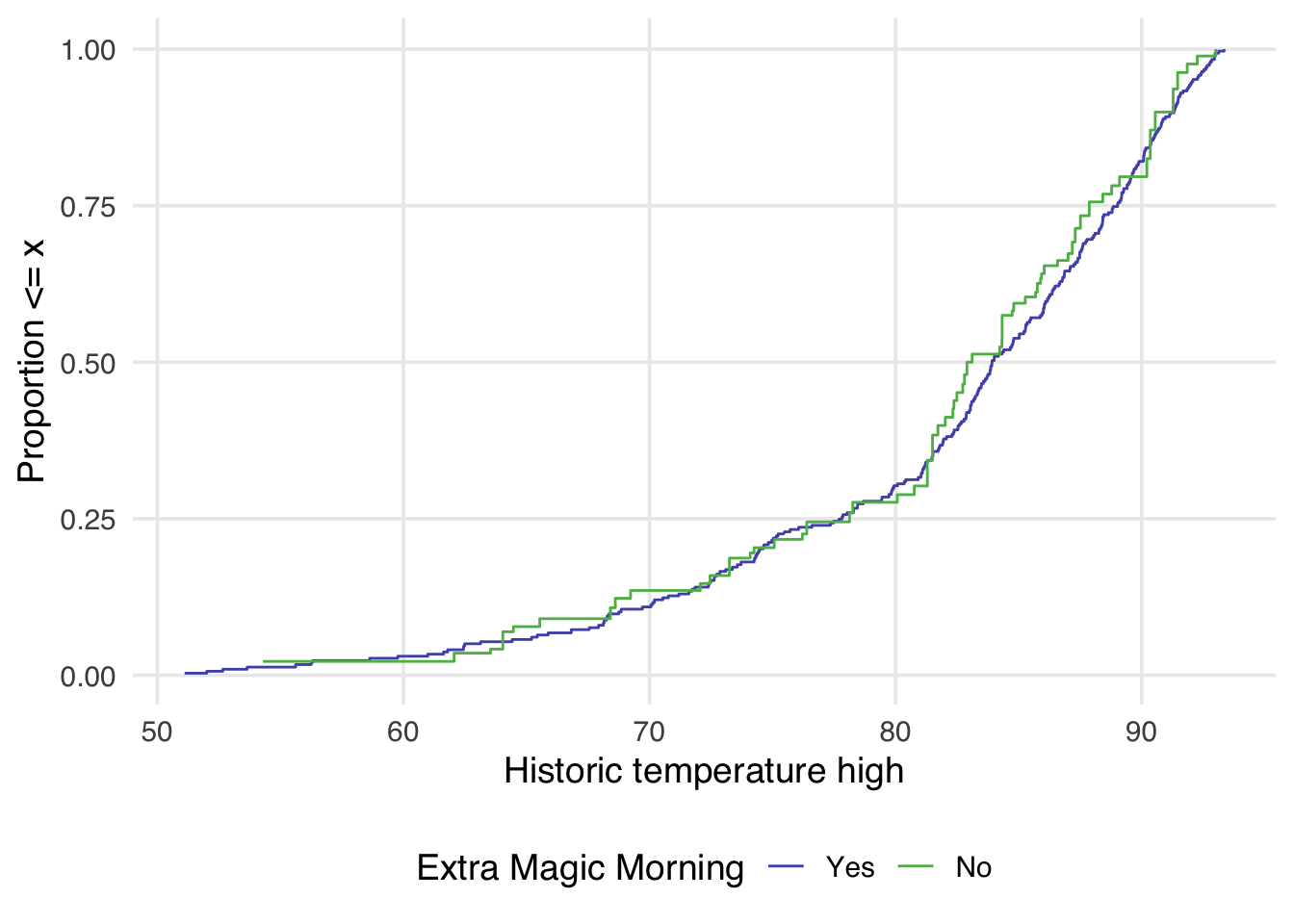
Now in Figure 9.5 the lines appear to overlap across the whole space.

9.3 Improving balance

9.3.1 Don’t use prediction metrics for causal modeling

By and large, metrics commonly used for building prediction models are inappropriate for building causal models. Researchers and data scientists often make decisions about models using metrics like R², AUC, accuracy, and (often inappropriately) p-values. However, a causal model’s goal is not to predict as much about the outcome as possible (Hernán and Robins 2021); the goal is to estimate the relationship between the exposure and outcome accurately. A causal model needn’t predict particularly well to be unbiased.

These metrics, however, may help identify a model’s best functional form. Generally, we’ll use DAGs and our domain knowledge to build the model itself. However, we may be unsure of the mathematical relationship between a confounder and the outcome or exposure. For instance, we may not know if the relationship is linear. Misspecifying this relationship can lead to residual confounding: we may only partially account for the confounder in question, leaving some bias in the estimate. Testing different functional forms using prediction-focused metrics can help improve the model’s accuracy, potentially allowing for better control.

Can you overfit a causal model?

In predictive modeling, data scientists often have to prevent overfitting their models to chance patterns in the data. When a model captures those chance patterns, it doesn’t predict as well on other data sets. So, can you overfit a causal model?

The short answer is yes, although it’s easier to do it with machine learning techniques than with logistic regression and friends. An overfit model is, essentially, a misspecified model (Gelman 2017). A misspecified model will lead to residual confounding and, thus, a biased causal effect. Overfitting can also exacerbate stochastic positivity violations (Zivich, Cole, and Westreich 2022). The correct causal model (the functional form that matches the data-generating mechanism) cannot be overfit. The same is true for the correct predictive model.

There’s some nuance to this answer, though. Overfitting in causal inference and prediction is different; we’re not applying the causal estimate to another dataset (the closest to that is transportability and generalizability, an issue we’ll discuss in Chapter 24). It remains true that a causal model doesn’t need to predict particularly well to be unbiased.

In prediction modeling, people often use a bias-variance trade-off to improve out-of-data predictions. In short, some bias for the sample is introduced to improve the variance of model fits and make better predictions out of the sample. However, we must be careful: the word bias here refers to the discrepancy between the model estimates and the true value of the dependent variable in the dataset. Let’s call this statistical bias. It is not necessarily the same as the difference between the model estimate and the true causal effect in the population. Let’s call this causal bias. If we apply the bias-variance trade-off to causal models, we introduce statistical bias in an attempt to reduce causal bias. Another subtlety is that overfitting can inflate the standard error of the estimate in the sample, which is not the same variance as the bias-variance trade-off (Schuster, Lowe, and Platt 2016). From a frequentist standpoint, the confidence intervals will also not have nominal coverage (see Appendix A) because of the causal bias in the estimate.

In practice, cross-validation, a technique to reduce overfitting, is often used with causal models that use machine learning, as we’ll discuss in Chapter 21.